La capacité des molécules d'ADN à participer à des mécanismes de réplication et de transcription ainsi qu'à s'organiser en chromosomes doit beaucoup à leur élasticité. Ainsi, l'étude de la réaction d'une molécule d'ADN aux contraintes mécaniques permet d'éclairer les processus biologiques mis en œuvre dans une cellule vivante. À l'aide d'une expérience et de deux modèles mécaniques d'un brin d'ADN, ce sujet propose de caractériser l'élasticité de l'ADN. Pour cela, on suppose qu'on exerce une traction sur un brin d'ADN et on cherche à établir une relation entre la force utilisée et l'allongement de la molécule.

Le seul langage de programmation autorisé dans cette épreuve est Python. Pour répondre à une question, il est possible de faire appel aux fonctions définies dans les questions précédentes. Dans tout le sujet on suppose que les bibliothèques math, numpy et random ont été importées grâce aux instructions

import math
import numpy as np
import random

Si les candidats font appel à des fonctions d'autres bibliothèques, ils doivent préciser les instructions d'importation correspondantes.
Ce sujet utilise la syntaxe des annotations pour préciser le type des arguments et du résultat des fonctions à écrire. Ainsi

def maFonction(n:int, X:[float], c:str, u) -> (int, np.ndarray):

signifie que la fonction maFonction prend quatre arguments, le premier ( n ) est un entier, le deuxième ( X ) une liste de nombres à virgule flottante, le troisième (c) une chaine de caractères et le type du dernier (u) n'est pas précisé. Cette fonction renvoie un couple dont le premier élément est un entier et le deuxième un tableau numpy. Il n'est pas demandé aux candidats de recopier les entêtes avec annotations telles qu'elles sont fournies dans ce sujet, ils peuvent utiliser des entêtes classiques. Ils veilleront cependant à décrire précisément le rôle des fonctions qu'ils définiraient eux-mêmes.
Dans ce sujet, le terme «liste» appliqué à un objet Python signifie qu'il s'agit d'une variable de type list. Les termes «vecteur» et «tableau» désignent des objets numpy de type np.ndarray, respectivement à une dimension ou de dimension quelconque. Enfin le terme «séquence» représente une suite itérable et indiçable, indépendamment de son type Python, ainsi un tuple d'entiers, une liste d'entiers et un vecteur d'entiers sont tous trois des «séquences d'entiers ».
Une attention particulière sera portée à la lisibilité, la simplicité et l'efficacité du code proposé. En particulier, l'utilisation d'identifiants significatifs, l'emploi judicieux de commentaires et la description du principe de chaque programme seront appréciés.
Une liste de fonctions utiles est fournie à la fin du sujet.

I Fonctions utilitaires

Cette partie définit quelques fonctions qui pourront avantageusement être utilisées dans la suite du sujet.
Q 1. Écrire une fonction d'entête
def moyenne(X) -> float:
qui prend en paramètre une séquence de nombres et qui calcule la moyenne de ces nombres. Cette fonction ne doit pas modifier le paramètre X .
Par exemple : moyenne([1, 2, 3, 4]) -> 2.5

Q 2. Écrire une fonction d'entête
def variance(X) -> float:
qui calcule la variance d'une séquence de nombres, sans la modifier. Pour rappel, la variance des n nombres

est la moyenne des carrés des écarts à la moyenne, c'est-à-dire

Par exemple: variance([1, 2, 3, 4]) -> 1.25
Q 3. Écrire une fonction d'entête
def somme(M):
qui prend en paramètre une séquence imbriquée, de profondeur et de structure quelconques, dont tous les composants élémentaires sont des nombres, et calcule la somme de tous ces éléments.
Par exemple : somme

Indication - L'expression booléenne isinstance ( x , numbers. Real) permet de tester si x est un scalaire numérique. Par exemple
isinstance(1, numbers.Real) -> True
isinstance(2.3e4, numbers.Real) -> True
isinstance([1, 2, 3], numbers.Real) -> False

II Mesures expérimentales

Depuis quelques décennies, des équipes de recherche réussissent à isoler un brin d'ADN et à mesurer ses propriétés mécaniques. Cette partie s'appuie sur une série d'expériences réalisées dans les années 1990, en particulier au laboratoire de physique statistique de l'École Normale Supérieure.
Une molécule d'ADN est attachée à une de ses extrémités sur un support transparent, une microbille magnétique de diamètre

est greffée à son autre extrémité. À l'aide d'aimants, la molécule d'ADN est soumise à une force de traction notée

. Afin de caractériser l'élasticité du brin d'ADN, on cherche à mesurer son allongement pour différentes intensités de la force de traction.
L'intensité de la force de traction n'est pas accessible directement, nous allons l'évaluer indirectement. Une fois le brin d'ADN mis en tension, son extrémité matérialisée par la bille ne reste pas immobile, elle est animée d'un mouvement aléatoire, dit mouvement brownien, dû à l'agitation des molécules du liquide qui l'entourent. En assimilant la molécule à un ressort, on montre que l'intensité de la force de traction est inversement proportionnelle aux fluctuations quadratiques moyennes de la position de la bille.
Une caméra CCD reliée à un ordinateur permet de photographier l'image de la bille (figure 1). Compte tenu de la taille de cette bille, on obtient une image de diffraction que nous allons analyser pour déterminer la position de la bille.

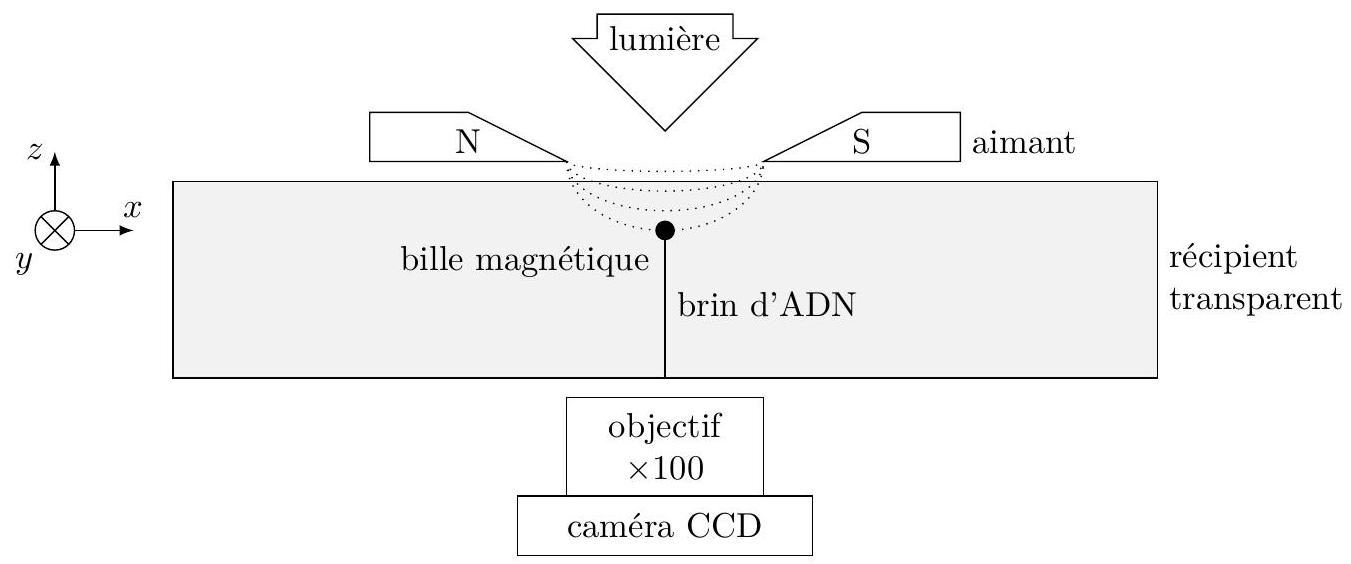
Figure 1 Schéma du dispositif expérimental (échelle non respectée)

II.A - Position de la bille

La figure 2 donne, à gauche, un exemple d'image obtenue par la caméra CCD. Cette caméra est pilotée par un programme Python qui récupère chaque image sous la forme d'un tableau d'entiers à deux dimensions. Les images obtenues sont en niveau de gris, chaque pixel est codé sur 8 bits, soit une valeur comprise entre 0 (noir) et 255 (blanc).

Afin de repérer le centre de la figure de diffraction, l'image est convertie en noir et blanc inversé suivant une valeur seuil du niveau de gris : les pixels au-dessus du seuil deviennent noirs, ceux en dessous deviennent blancs. Une fois ce seuillage effectué, on calcule le barycentre des pixels blancs de l'image seuillée pour obtenir la position de la bille.
On rappelle que l'abscisse (respectivement ordonnée) du barycentre d'un ensemble de points de même poids est la moyenne des abscisses (respectivement ordonnées) des points considérés.

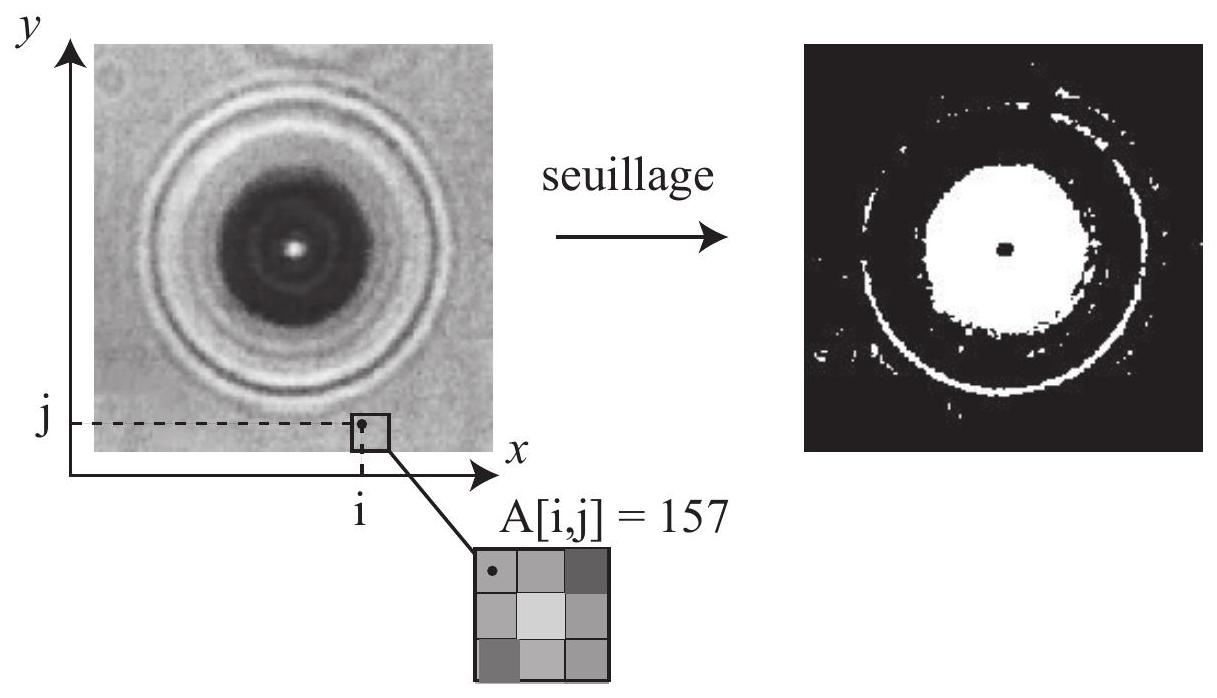
Figure 2 Figure de diffraction d'une bille et opération de seuillage

Q 4. Écrire une fonction d'entête
def seuillage(A:np.ndarray, seuil:int) -> np.ndarray:
qui prend en paramètre un tableau d'entiers à deux dimensions représentant un cliché de la caméra CCD et construit un tableau de même forme contenant la valeur 1 là où la valeur des pixels de l'image originale est strictement inférieure au seuil et la valeur 0 ailleurs (pixels supérieurs ou égaux au seuil).
Q 5. Écrire une fonction d'entête
def pixel_centre_bille(A:np.ndarray) -> (int, int):
qui prend en paramètre l'image seuillée telle que produite par la fonction seuillage et renvoie les indices (ligne et colonne) du pixel le plus proche du centre de la bille (barycentre des pixels à 1).

On dispose de la fonction d'entête
def prendre_photo() -> np.ndarray:
qui déclenche la prise d'un cliché par la caméra CCD et renvoie l'image prise sous la forme d'un tableau à deux dimensions tel que décrit plus haut.
Q 6. Écrire une fonction d'entête
def positions(n:int, seuil:int) -> [(int, int)]:
qui prend n photographies de la bille et renvoie la liste de ses positions dans chaque photographie en seuillant les images à la valeur seuil. Le résultat de cette fonction est donc une liste de n couples de deux entiers correspondants à l'indice de ligne et de colonne des positions successives du centre de la bille au cours de son mouvement brownien.

Le capteur CCD est positionné parallèlement au plan

et ses pixels sont carrés. La caméra a été calibrée dans les conditions de l'expérience : un pixel correspond à un carré du plan (

) de côté

.
Q 7. Définir une fonction d'entête
def fluctuations(P:[(int, int)], t:float) -> float:
qui prend en paramètre une liste de positions successives de la bille (telle que produite par la fonction positions) et la longueur correspondant à un pixel et calcule la valeur moyenne des déplacements quadratiques de la bille : moyenne des carrés des écarts entre chaque position mesurée et la position d'équilibre de la bille (correspondant au barycentre des différentes positions observées).

II.B - Allongement du brin d'ADN

La position de la bille étant déterminée dans le plan (

), nous allons maintenant nous intéresser à sa cote, c'est-à-dire sa position dans la direction perpendiculaire à la caméra.
Pour déterminer la position de la bille suivant

, nous utilisons une méthode basée sur la répartition des cercles de la figure de diffraction. Pour cela, nous construisons un profil de cette figure en découpant l'image seuillée en anneaux concentriques centrés sur la position de la bille. Le décompte de la proportion de pixels blancs dans chaque anneau fournit un profil de la figure de diffraction qui permet de calculer la cote

de la bille en tenant compte des paramètres de calibration de la caméra.

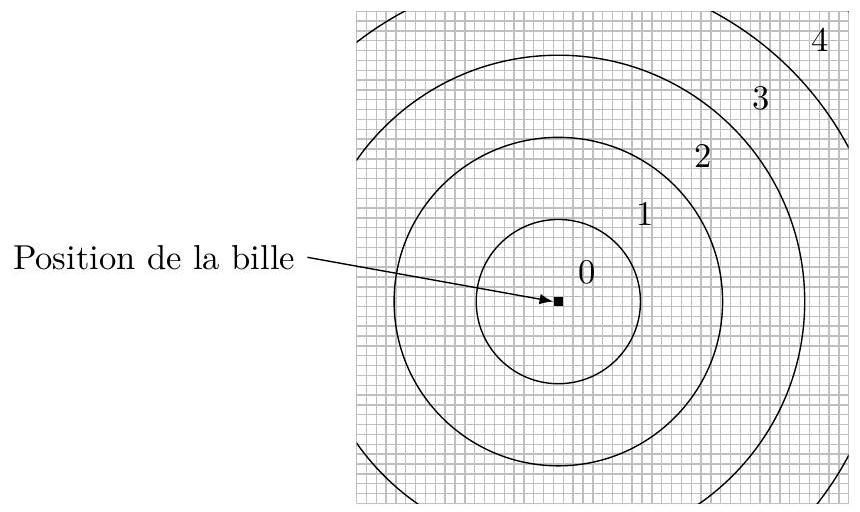
Figure 3 Exemple de découpage d'une image en cinq anneaux concentriques

Q 8. Écrire une fonction d'entête
def profil(A:np.ndarray, n:int):
qui construit le profil d'une figure de diffraction seuillée A en la découpant en n anneaux concentriques. Cette fonction renvoie, au choix du candidat, un vecteur ou une liste de n nombres, compris entre 0 et 1 , qui donne la proportion de pixels blancs compris dans chaque anneau. Un pixel sera considéré comme contenu dans un anneau si son centre s'y trouve. L'élément d'indice 0 du résultat correspond à la bande la plus proche du centre de la figure (position de la bille).
Afin de clarifier l'écriture du code, il peut être pertinent de définir des fonctions intermédiaires pour programmer la fonction profil. Les candidats veilleront à expliquer précisément le rôle de chaque fonction intermédiaire qu'ils définiraient.
Q 9. Si on travaille sur une image carrée de dimension

pixels, quelle est la complexité de la fonction profil en fonction de

et de

(nombre d'anneaux) ?

II.C - Synthèse

Pour une configuration expérimentale donnée, il est ainsi possible en prenant une série de clichés de déterminer l'amplitude du mouvement brownien de l'extrémité du brin d'ADN ainsi que sa position en trois dimensions. Ces éléments permettent alors de déterminer l'intensité de la force de traction appliquée au brin d'ADN ainsi que son allongement.
En modifiant les aimants, on peut faire varier l'intensité du champ magnétique et donc la force appliquée au brin d'ADN. En renouvelant l'expérience, on obtient ainsi une série de points expérimentaux correspondant à diverses valeurs de force et d'allongement.

III Modèle du ver

Le «modèle du ver» est un modèle souvent utilisé pour décrire le comportement mécanique de certains polymères. Dans ce modèle, la molécule étudiée est représentée par une succession de segments semi-rigides orientés grossièrement dans la même direction. Il permet d'obtenir une expression simplifiée de

, l'intensité de la force de traction

, en fonction de

, l'allongement de la molécule :

où

est la constante de Boltzman et

la température. Ce modèle est paramétré par deux longueurs :

, longueur de persistance représentant la longueur typique sur laquelle le polymère maintient sa forme malgré les déformations dues à l'agitation thermique ;
, extension maximale du polymère.

III.A - Calcul des paramètres

Ces deux grandeurs ne sont pas accessibles directement pour une molécule d'ADN. L'objectif de cette partie est de déterminer les valeurs de

correspondant au brin d'ADN objet des mesures développées dans la partie précédente.
Pour cela nous utilisons la fonction curve_fit du package scipy.optimize qui permet d'ajuster les paramètres d'une courbe afin qu'elle passe au plus proche d'un certain nombre de points. La fonction curve_fit utilise pour cela une méthode de moindres carrés non linéaire. Une adaptation de la documentation de cette fonction est fournie par la figure 4.

popt, pcov = scipy.optimize.curve_fit(f, xdata, ydata)
Paramètres
- f:callable
    La fonction modèle, f (x, ...). Elle doit prendre la variable indépendante comme premier argument
    et chaque paramètre à ajuster comme argument suivant.
- xdata: séquence de longueur M
    La liste des valeurs de la variable indépendante correspondant aux différentes mesures.
- ydata: séquence de longueur M
    Les mesures, typiquement f(xdata, ...).
Résultat
- popt: tableau
    Valeurs optimales des paramètres telles que la somme des carrés des écarts f (xdata, *popt) - ydata
    soit minimale.
- pcov:tableau à deux dimensions
    Une estimation de la covariance de popt. Les termes diagonaux donnent la variance de l'estimateur du
    paramètre correspondant.
    Pour estimer l'écart-type de l'erreur sur les paramètres, on peut utiliser perr = np.sqrt(np.diag(pcov)).

Figure 4 Extrait adapté de la documentatin de curve_fit

Q 10. Écrire une fonction d'entête

def force(z:np.ndarray, Lp:float, L0:float, T:float) -> np.ndarray:

qui calcule la force donnée par la formule (III.1) pour chaque élément du vecteur z. Cette fonction renvoie un vecteur de même taille que

contenant le résultat du calcul pour chaque composante de

. La variable globale K_B fournit la valeur de la constante de Boltzman.

On dispose d'une série de points expérimentaux issus d'essais réalisés suivant les modalités décrites dans le II.C. Ces valeurs expérimentales sont stockées dans un tableau à deux dimensions. Chaque ligne (première dimension) contient le résultat d'une mesure, la première colonne donne la valeur obtenue pour la force et la deuxième celle de l'allongement.
Q 11. Écrire une fonction d'entête
def ajusteWLC(Fz:np.ndarray, T:float) -> (float, float):
qui ajuste les paramètres de la formule (III.1) pour qu'ils correspondent au mieux aux valeurs expérimentales du tableau Fz obtenues par une série d'essais effectués à la température T. Cette fonction renvoie un couple de nombres donnant les valeurs optimales de

et de

III.B - Algorithme de minimum local

La fonction curve_fit permet d'utiliser différents algorithmes d'optimisation. Nous allons jeter les bases d'un algorithme permettant d'obtenir les valeurs optimales

III.B.1) Implantation d'un algorithme de minimisation 1D

Soit

une fonction de classe

sur

présentant un minimum local.
On rappelle que

est une expression approchée d'ordre 2 de la dérivée de

(notée

On suppose que l'ordinateur utilisé représente les nombres flottants sur 64 bits avec un bit de signe, 11 bits d'exposant et 52 bits de mantisse.
Q 12. Calculer le nombre de chiffres significatifs décimaux donnés par ce codage.
Q 13. Justifier que les valeurs

ne permettent pas obtenir une bonne approximation du nombre dérivé

. Proposer alors une valeur adaptée de

.
Q 14. Écrire une fonction d'entête
def derive(phi, x:float, h:float) -> float:
qui calcule une valeur approchée de la dérivée au point x de phi, fonction réelle d'une variable réelle, où h correspond au

de la formule (III.2).
Q 15. Écrire une fonction d'entête
def derive_seconde(phi, x:float, h:float) -> float:
permettant d'obtenir une approximation de la dérivée seconde de la fonction phi au point

.
Q 16. Écrire une fonction d'entête
def min_local(phi, x0:float, h:float) -> float:
basée sur la méthode de Newton permettant de trouver l'abscisse d'un minimum local de la fonction phi. La valeur approchée de cette abscisse vérifiera

III.B.2) Implantation d'un algorithme de minimisation 2D

L'écart quadratique entre les valeurs expérimentales de la force

correspondant à l'élongation

et les valeurs de la fonction force est défini par

Les valeurs optimales de

correspondent au minimum de la fonction

, c'est-à-dire à un point où son gradient est nul. Pour déterminer le point

correspondant au minimum de la fonction

, nous allons adapter la méthode de Newton unidimensionnelle pour rechercher un zéro d'une fonction de deux variables puis appliquer cette méthode au gradient de

On considère

une fonction réelle de deux variables réelles

de classe

sur

, présentant un minimum local. On note

les composantes du gradient de la fonction

. On rappelle que

L'objectif est d'approcher les valeurs

qui annulent les fonctions

et correspondent donc à un extremum de la fonction

, en partant d'un point arbitraire (

).
Q 17. Montrer que les coordonnées (

) du point situé à l'intersection des plans

tangent à la surface au point ,
tangent à la surface au point ,
d'équation ,
vérifient la relation suivante où on explicitera l'expression de :

Si la matrice

est inversible, en s'inspirant de la méthode de Newton, on construit une relation de récurrence sous la forme :

Nous allons utiliser cette relation pour recherche le minimum local d'une fonction réelle de deux variables réelles implantée en Python sous la forme d'une fonction prenant en paramètre une séquence de deux nombres. Par exemple

def fct_dont_je_veux_le_minimum(X:np.ndarray) -> float:

Q 18. Écrire une fonction d'entête
def

np.ndarray:
qui fournit une approximation de la valeur du gradient de la fonction réelle de deux variables réelles G au point

en utilisant h comme paramètre pour le calcul approché des dérivées, voir formule (III.2).
Q 19. Écrire une fonction d'entête
def min_local_2D(G, X0:np.ndarray, h:float) -> np.ndarray:
permettant d'obtenir une approximation numérique des valeurs de

correspondant à un minimum local de la fonction G en partant du point

et en utilisant h comme paramètre pour le calcul approché des dérivées. La valeur approchée du minimum local vérifiera

IV Modèle de la chaine librement jointe

La molécule d'ADN peut également être représentée par le modèle de la «chaine librement jointe» dans laquelle des segments rigides (appelés monomères) sont liés à leurs extrémités et librement orientables aux points de jointure. On appelle conformation de la molécule sa configuration géométrique. En l'absence d'action extérieure, l'orientation de chaque segment par rapport à ses voisins est aléatoire et toutes les conformations sont équiprobables.
Ce modèle supposant une part d'aléa, il n'est plus possible, comme dans le modèle du ver, d'obtenir une formule liant directement la force et l'allongement. Nous allons donc utiliser un programme informatique pour simuler le comportement de ce modèle de molécule et obtenir l'allongement en fonction de la force utilisée.
La simulation proposée est basée sur la méthode dite de «Monte Carlo » faisant participer nombres aléatoires, statistiques et probabilités. Dans le sens plus spécifique des simulations moléculaires, un modèle de la molécule est développé pour calculer une énergie, puis des changements aléatoires sont effectués pour converger vers l'état naturel de la molécule. Une fois la convergence atteinte, des calculs statistiques permettent d'approximer les paramètres cherchés.
Par souci de simplicité, nous travaillons dans un espace à deux dimensions.

IV.A - Modélisation plane

La molécule comporte

monomères de longueur

. On note

l'angle formé par le segment

avec la direction de la force

. Les angles

définissent la conformation de la molécule (figure 5).

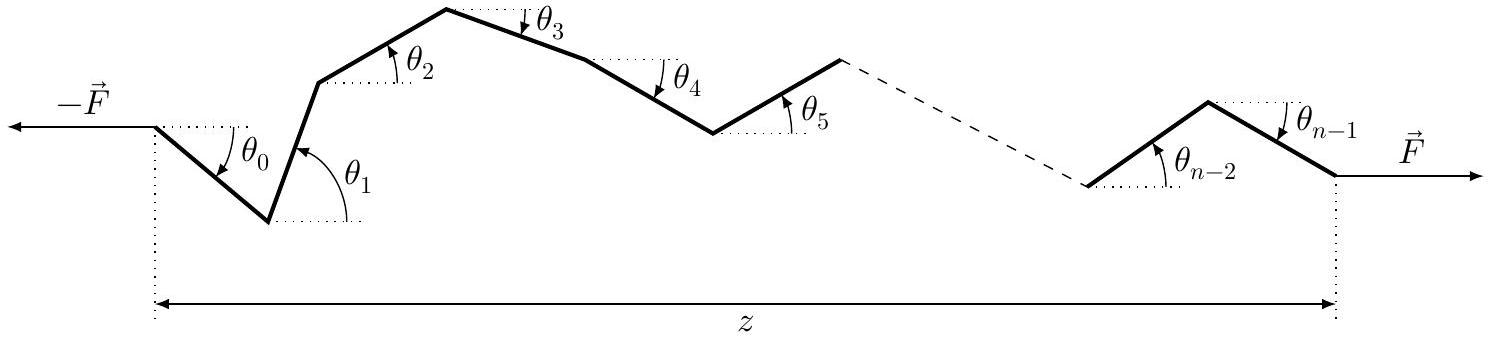
Figure 5 Représentation d'un brin d'ADN sous forme de chaine librement jointe

Pour un brin d'ADN soumis à une force

imposée, l'énergie mécanique

développée pour étendre la molécule s'écrit

où

est l'intensité de la force et

l'allongement de la molécule suivant la direction de la force (figure 5).
La simulation démarre à partir d'une conformation aléatoire du brin d'ADN.
Q 20. Écrire une fonction d'entête
def conformation(n:int):
qui génère une conformation aléatoire d'un brin d'ADN composé de n segments. Cette fonction renvoie une liste ou un vecteur de longueur n correspondant à l'orientation (angle

) de chaque segment.
Q 21. Écrire une fonction d'entête
def allongement(theta, l:float) -> float:
qui calcule l'allongement

de la chaine dans la conformation theta pour une longueur de segment 1 .

La modification de la conformation se fait en modifiant de façon aléatoire

angles successifs,

étant un paramètre de simulation ajustable.
Q 22. Écrire une fonction d'entête
def nouvelle_conformation(theta, k:int):
qui crée une nouvelle conformation, à partir de la conformation theta en modifiant k valeurs successives à partir d'un indice aléatoire.

IV.B - Critère de Metropolis Monte Carlo (MMC)

La méthode spécifique utilisée dans la plupart des études génétiques a été développée par Metropolis et al. en 1953. Une probabilité

simule l'agitation thermique de la molécule. Cette agitation tend à désordonner la molécule (maximum d'entropie), alors que la force extérieure tend à aligner les brins (diminution de l'entropie). Les deux phénomènes convergent vers une situation d'équilibre statistique, où force et allongement moyen sont liés. L'algorithme vise à déterminer cet équilibre statistique.
À partir d'une conformation de départ, d'énergie calculée

, une nouvelle conformation est crée et son énergie

est calculée. Si cette nouvelle conformation possède une énergie inférieure à celle de son précurseur

, elle est conservée. Si

, la nouvelle conformation est conservée, avec la probabilité

où

est la constante de Boltzman et

la température. Si la nouvelle conformation est rejetée, c'est la conformation de départ, d'énergie

, qui est conservée pour la suite de la simulation.
Q 23. Écrire une fonction d'entête
def selection_conformation(thetaA, thetaB, F:float, l:float, T:float):
qui prend en paramètre deux conformations successives thetaA et thetaB (thetaA étant le précurseur de thetaB) et renvoie la conformation conservée connaissant

, l'intensité de la force de traction, 1 la longueur d'un monomère et T la température.

IV.C - Implantation de la simulation

L'algorithme est supposé avoir convergé lorsque la variance de l'allongement du brin d'ADN sur les 500 dernières itérations est inférieure à une valeur

, paramètre de la simulation.
Q 24. Écrire une fonction d'entête
def monte_carlo(F:float, n:integer, l:float, T:float, k:integer, epsilon:float) -> float:
qui simule l'application d'une force de traction d'intensité F sur un brin d'ADN de n monomères de longueur 1 , à la température

. Les arguments

et epsilon correspondent aux paramètres de la simulation présentés plus haut. Le résultat de la fonction est l'allongement moyen des 500 dernières conformations, une fois la convergence atteinte.
Les candidats ont la liberté de concevoir et d'utiliser les structures de données qui leur semblent les mieux adaptées à la programmation de la fonction monte_carlo. Ils veilleront à préciser le rôle et l'organisation des données manipulées qui ne seraient pas déjà décrites dans le sujet.
Indication - Compte tenu du nombre d'itérations envisagées, il est prudent de ne pas enregistrer toutes les étapes intermédiaires de la simulation. On pourra considérer l'utilisation d'une file pour stocker les données utiles à la simulation. À contrario d'une pile, une file est une structure de données où les premiers éléments ajoutés à la file sont les premiers à en être retirés («First In First Out»). En Python, une liste peut être utilisée pour représenter une file grâce aux opérations append et pop(0).

Une fois la fonction monte_carlo développée, il est trivial de l'utiliser pour simuler différentes intensités de la force et obtenir l'allongement correspondant du brin d'ADN simulé.

Opérations et fonctions Python disponibles

Fonctions

range( n ) renvoie la séquence des n premiers entiers ( )
list(range(5))
random. randrange(a, b) renvoie un entier aléatoire compris entre et inclus (a et b entiers)
random.random() renvoie un nombre flottant tiré aléatoirement dans [ 0,1 [ suivant une distribution uniforme
random. shuffle(u) permute aléatoirement les éléments de la liste u (modifie u)
random.sample(u, n) renvoie une liste de n éléments distincts de la liste u choisis aléatoirement, si n > len (u), déclenche l'exception ValueError
math.sqrt(x) calcule la racine carrée du nombre x
round(n) arrondit le nombre n à l'entier le plus proche
math.ceil(x) renvoie le plus petit entier supérieur ou égal à x
math.floor(x) renvoie le plus grand entier inférieur ou égal à

Opérations sur les listes

len(u) donne le nombre d'éléments de la liste u:
construit une liste constituée de la concaténation des listes et :
construit une liste constituée de la liste u concaténée fois avec elle-même :
e in et e not in déterminent si l'objet e figure dans la liste , cette opération a une complexité temporelle en
2 in True ; 2 not in [1, 2, 3] False
u.append(e) ajoute l'élément e à la fin de la liste (similaire à )
u.pop(i): renvoie l'élément à l'indice i de la liste u et le supprime
del u[i] supprime de la liste u son élément d'indice i
del supprime de la liste tous ses éléments dont les indices sont compris dans l'intervalle [i,j[
u.remove(e) supprime de la liste u le premier élément qui a pour valeur e, déclenche l'exception ValueError si e ne figure pas dans u, cette opération a une complexité temporelle en
u.insert (i, e) insère l'élément e à la position d'indice i dans la liste u (en décalant les éléments suivants) ; si i >= len(u), e est ajouté en fin de liste
permute les éléments d'indice et dans la liste

Opérations sur les tableaux (np.ndarray)

np.array(u) crée un nouveau tableau contenant les éléments de la séquence u. La taille et le type des éléments de ce tableau sont déduits du contenu de u
np.empty( , dtype), np.empty( ), dtype) crée respectivement un vecteur à éléments ou un tableau à n lignes et m colonnes dont les éléments, de valeurs indéterminées, sont de type dtype qui peut être un type standard (bool, int, float, ...) ou un type spécifique numpy (np.int16, np.float32, ...). Si le paramètre dtype n'est pas précisé, il prend la valeur float par défaut
np.zeros(n, dtype), np.zeros((n, m), dtype) fonctionne comme np.empty en initialisant chaque élément à la valeur zéro pour les types numériques ou False pour les types booléens
a.ndim nombre de dimensions du tableau a
a.shape tuple donnant la taille du tableau a pour chacune de ses dimensions
len(a) taille du tableau a dans sa première dimension, équivalent à a.shape[0]
a.size nombre total d'éléments du tableau a
a.flat itérateur sur tous les éléments du tableau a
np.ndenumerate(a) itérateur sur tous les couples (index, élément) du tableau a où «index» est un tuple de a.ndim entiers donnant les indices de l'élément
a.min(), a.max() renvoie la valeur du plus petit (respectivement plus grand) élément du tableau a; ces opérations ont une complexité temporelle en (a.size)
b in a détermine si b est un élément du tableau a ; si b est un scalaire, vérifie si b est un élément de a ; si est un vecteur ou une liste et un tableau à deux dimensions, détermine si est une ligne de
np.concatenate((a1, a2)) construit un nouveau tableau en concaténant deux tableaux selon leur première dimension ; a1 et a2 doivent avoir le même nombre de dimensions et la même taille à l'exception de leur taille dans la première dimension (deux tableaux à deux dimensions doivent avoir le même nombre de colonnes pour pouvoir être concaténés)
np.transpose(a) renvoie le transposé du tableau a
np.dot(a, b) calcule le produit matriciel des tableaux a et b
np.linalg.inv(a) renvoie l'inverse du tableau a, lève l'exception ValueError si a n'est pas un tableau carré à deux dimensions et LinAlgError si a n'est pas inversible