Version interactive avec LaTeX compilé
Les calculatrices sont interdites.
NB. : Le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction.
Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.
Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.
Ce sujet comporte deux problèmes qui pourront être traités séparément.
Le candidat est invité à remarquer que ces deux problèmes sont de longueur inégale, le second problème étant deux fois plus long que le premier.
Le candidat est invité à remarquer que ces deux problèmes sont de longueur inégale, le second problème étant deux fois plus long que le premier.
Problème
Dans ce problème, les vecteurs sont notés en caractères gras
Le but de cette partie est de calculer le champ magnétique au centre d'un triangle équilatéral parcouru par un courant I. Les fils d'alimentation du courant I ne sont pas représentés et leur influence est négligée.
- Soit un segment de fil rectiligne conducteur de longueur finie OA suivant
, parcouru par un courant I dont le sens est représenté figure 1.
a) Pourquoi ne peut-on pas appliquer le théorème d'Ampère au segment OA ?
b) En utilisant la loi de Biot et Savart, calculer le champ magnétiqueen un point créé par ce fil. On donnera le résultat sous sa forme la plus simple, fonction d'un vecteur unitaire, de I, et où est la perméabilité du vide, et les angles représentés sur la figure 1 . - Déduire de l'expression précédente le champ magnétique
créé par un fil de longueur infinie en fonction de et d'un vecteur unitaire. - Dans le cas d'un fil de longueur infinie, retrouver le résultat de la question 2 en utilisant des considérations de symétrie, puis en appliquant le théorème d'Ampère à un contour judicieusement choisi.
- Déduire de la question 1. le champ magnétique
créé au centre C d'un triangle équilatéral de côté AB , parcouru par un courant I dont le sens est représenté figure 2 . On donnera le résultat en fonction de et d'un vecteur unitaire.
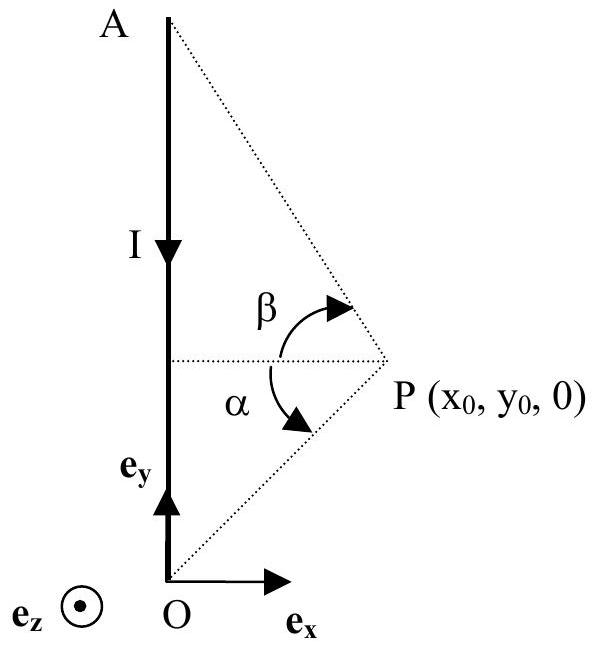
Figure 1
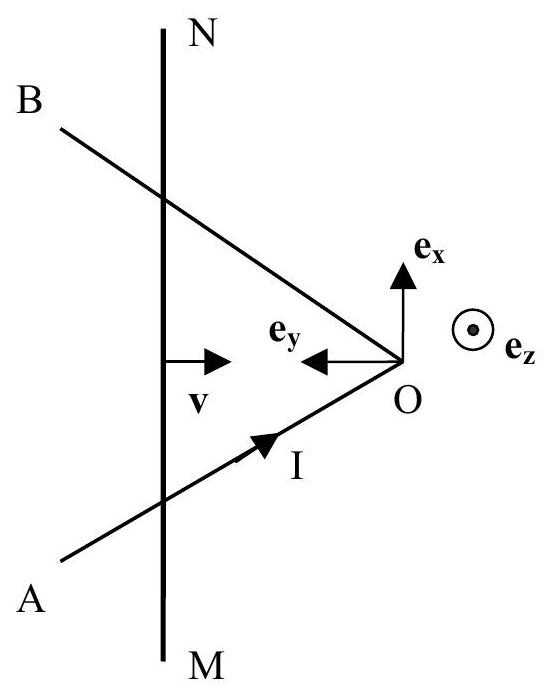
Figure 3
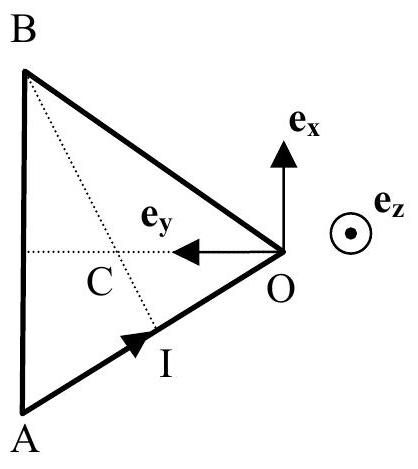
Figure 2
2ème partie: Phénomènes d'induction
Deux rails OA et OB , filiformes, fixes, de longueur commune
Une barre filiforme MN , de masse m , se déplace sans frottement sur les rails d'un mouvement de translation parallèle à
Les 2 rails et la barre ont la même résistivité linéique
L'ensemble du dispositif est plongé dans un champ magnétique extérieur
5. On considère le déplacement de la barre MN entre AB et O .
a) Déterminer la résistance du circuit en fonction de
b) Déterminer le flux de
c) En déduire la force électromotrice induite dans le circuit en fonction de
d) En écrivant l'équation électrique du circuit fermé ainsi formé, en déduire le courant I induit dans le circuit en fonction de
6.
a) Déterminer la force de Laplace
b) En déduire la force
7. Calculer la puissance de cette force, puis la puissance dissipée par effet Joule. Que peut-on en conclure?
8. La barre partant de
Une barre filiforme MN , de masse m , se déplace sans frottement sur les rails d'un mouvement de translation parallèle à
Les 2 rails et la barre ont la même résistivité linéique
L'ensemble du dispositif est plongé dans un champ magnétique extérieur
5. On considère le déplacement de la barre MN entre AB et O .
a) Déterminer la résistance du circuit en fonction de
b) Déterminer le flux de
c) En déduire la force électromotrice induite dans le circuit en fonction de
d) En écrivant l'équation électrique du circuit fermé ainsi formé, en déduire le courant I induit dans le circuit en fonction de
6.
a) Déterminer la force de Laplace
b) En déduire la force
7. Calculer la puissance de cette force, puis la puissance dissipée par effet Joule. Que peut-on en conclure?
8. La barre partant de
Problème
Les parties 2 et 3 sont indépendantes.
1. Questions de cours
1.1. Donner la définition d'un système fermé.
Pour un système thermodynamique fermé, énoncer le second principe de la thermodynamique. On rappellera notamment le bilan entropique liant la variation d'entropie
Toute équation devra être accompagnée d'une explication.
1.2. Bilans entropiques particuliers
1.2.1. Donner la définition d'un système isolé.
Toute équation devra être accompagnée d'une explication.
1.2. Bilans entropiques particuliers
1.2.1. Donner la définition d'un système isolé.
Que devient le bilan entropique du 1.1. dans le cas d'un système isolé ?
1.2.2. Donner la définition d'un système stationnaire.
1.2.2. Donner la définition d'un système stationnaire.
Que devient le bilan entropique dans le cas d'un système stationnaire?
1.3. Donner deux exemples de causes d'irréversibilité.
1.4. Dans les questions suivantes, on notera
1.4.1. Exprimer la variation d'énergie interne d'un gaz parfait en fonction de la variation de la température.
1.4.2. Exprimer la variation d'entropie d'un gaz parfait en fonction des variations de température et de volume.
1.4.3. Dans le cas d'un gaz parfait, donner la relation entre
1.4.4. Exprimer
1.3. Donner deux exemples de causes d'irréversibilité.
1.4. Dans les questions suivantes, on notera
1.4.1. Exprimer la variation d'énergie interne d'un gaz parfait en fonction de la variation de la température.
1.4.2. Exprimer la variation d'entropie d'un gaz parfait en fonction des variations de température et de volume.
1.4.3. Dans le cas d'un gaz parfait, donner la relation entre
1.4.4. Exprimer
2. Compression d'un gaz parfait
Un cylindre circulaire d'axe vertical et de section
On notera
2.1. En étudiant l'équilibre du piston, donner l'expression de la pression
On notera
2.1. En étudiant l'équilibre du piston, donner l'expression de la pression
On ajoute dorénavant une surcharge de masse
2.2. On suppose dans cette question que le nouvel équilibre mécanique est atteint avant que tout échange de chaleur n'ait eu lieu avec l'extérieur.
2.2.1. Exprimer la pression
2.2.2. Déterminer le travail des forces de pression atmosphérique exercées sur le piston et transmises intégralement au gaz en fonction de
2.2.3. Déterminer le travail de pesanteur de l'ensemble {piston + surcharge} en fonction de
2.2.4. En appelant
2.2.5. En déduire alors
2.3. On suppose maintenant que l'équilibre thermique s'est établi avec l'extérieur.
2.2. On suppose dans cette question que le nouvel équilibre mécanique est atteint avant que tout échange de chaleur n'ait eu lieu avec l'extérieur.
2.2.1. Exprimer la pression
2.2.2. Déterminer le travail des forces de pression atmosphérique exercées sur le piston et transmises intégralement au gaz en fonction de
2.2.3. Déterminer le travail de pesanteur de l'ensemble {piston + surcharge} en fonction de
2.2.4. En appelant
2.2.5. En déduire alors
2.3. On suppose maintenant que l'équilibre thermique s'est établi avec l'extérieur.
Exprimer la pression
Exprimer ensuite la nouvelle position d'équilibre du piston
2.4. Quelle est la relation entre la quantité de chaleur
Donner l'expression du travail
2.5. On souhaite ici calculer les variations d'entropie sur l'ensemble de la transformation.
2.5.1. L'atmosphère extérieure ayant en permanence une température égale à
2.5.2. Quelle est l'entropie reçue par le gaz parfait dans le cylindre ? En utilisant la question 1.4.2, exprimer la variation d'entropie totale du gaz parfait dans le cylindre
2.5.3. En déduire la variation d'entropie de l'univers
2.5.4. La transformation est-elle réversible? Justifier la réponse.
2.6. On veut rendre cette fois-ci la transformation quasi statique, en ajoutant la surcharge de masse
Exprimer ensuite la nouvelle position d'équilibre du piston
2.4. Quelle est la relation entre la quantité de chaleur
Donner l'expression du travail
2.5. On souhaite ici calculer les variations d'entropie sur l'ensemble de la transformation.
2.5.1. L'atmosphère extérieure ayant en permanence une température égale à
2.5.2. Quelle est l'entropie reçue par le gaz parfait dans le cylindre ? En utilisant la question 1.4.2, exprimer la variation d'entropie totale du gaz parfait dans le cylindre
2.5.3. En déduire la variation d'entropie de l'univers
2.5.4. La transformation est-elle réversible? Justifier la réponse.
2.6. On veut rendre cette fois-ci la transformation quasi statique, en ajoutant la surcharge de masse
Lorsqu'on dépose la jième masse
2.6.1. Exprimer la variation d'entropie de l'univers
2.6.2. Exprimer sous la forme d'une somme la variation d'entropie de l'univers correspondant à l'ajout de toutes les petites masses.
En remarquant que
2.6.3. Que devient la variation d'entropie lorsque
2.6.1. Exprimer la variation d'entropie de l'univers
2.6.2. Exprimer sous la forme d'une somme la variation d'entropie de l'univers correspondant à l'ajout de toutes les petites masses.
En remarquant que
2.6.3. Que devient la variation d'entropie lorsque
3. Irréversibilité de la détente de Joule-Gay Lussac
3.1. Détente de Joule-Gay Lussac
On considère un récipient ayant des parois rigides et adiabatiques. Il est composé de deux compartiments de volume
3.1.1. Quel est le travail reçu par le gaz parfait au cours de la détente ?
3.1.2. Montrer que l'énergie interne du gaz est constante au cours de la détente.
3.1.3. En déduire que la température du gaz ne change pas au cours de la détente.
3.1.4. En utilisant la question 1.4.2., calculer la variation d'entropie du gaz au cours de la détente en fonction de
3.1.5. Que vaut l'entropie reçue par le gaz
3.2. On opère cette fois-ci de façon quasi statique à l'aide d'un récipient comportant
On souhaite procéder en augmentant le volume occupé par le gaz par petites quantités
3.2.1. Exprimer la variation d'entropie
3.2.2. Exprimer la variation d'entropie du gaz correspondant à la suppression de toutes les cloisons en fonction de
3.2.3. Comparer les résultats des questions 3.1.4. et 3.2.2.
3.1.1. Quel est le travail reçu par le gaz parfait au cours de la détente ?
3.1.2. Montrer que l'énergie interne du gaz est constante au cours de la détente.
3.1.3. En déduire que la température du gaz ne change pas au cours de la détente.
3.1.4. En utilisant la question 1.4.2., calculer la variation d'entropie du gaz au cours de la détente en fonction de
3.1.5. Que vaut l'entropie reçue par le gaz
3.2. On opère cette fois-ci de façon quasi statique à l'aide d'un récipient comportant
On souhaite procéder en augmentant le volume occupé par le gaz par petites quantités
3.2.1. Exprimer la variation d'entropie
3.2.2. Exprimer la variation d'entropie du gaz correspondant à la suppression de toutes les cloisons en fonction de
3.2.3. Comparer les résultats des questions 3.1.4. et 3.2.2.
En procédant de façon quasi statique, a-t-on rendu la transformation réversible ?
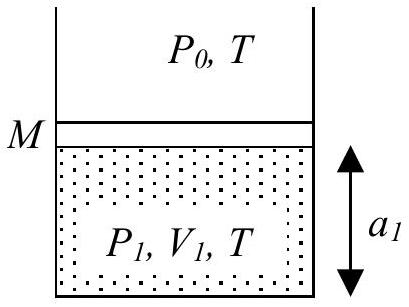
Fig. 1 : cylindre et piston dans la configuration initiale
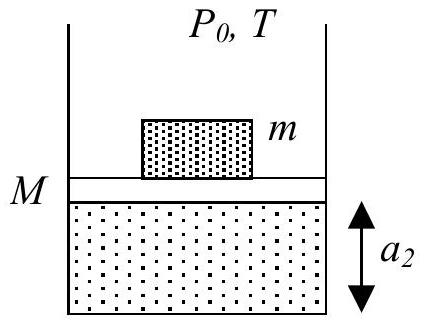
Fig. 2 : Ajout de la masse
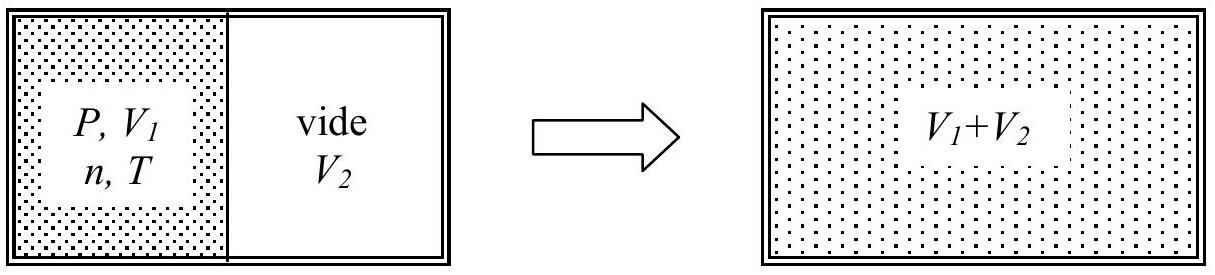
Fig. 3 : détente de Joule Gay-Lussac simple
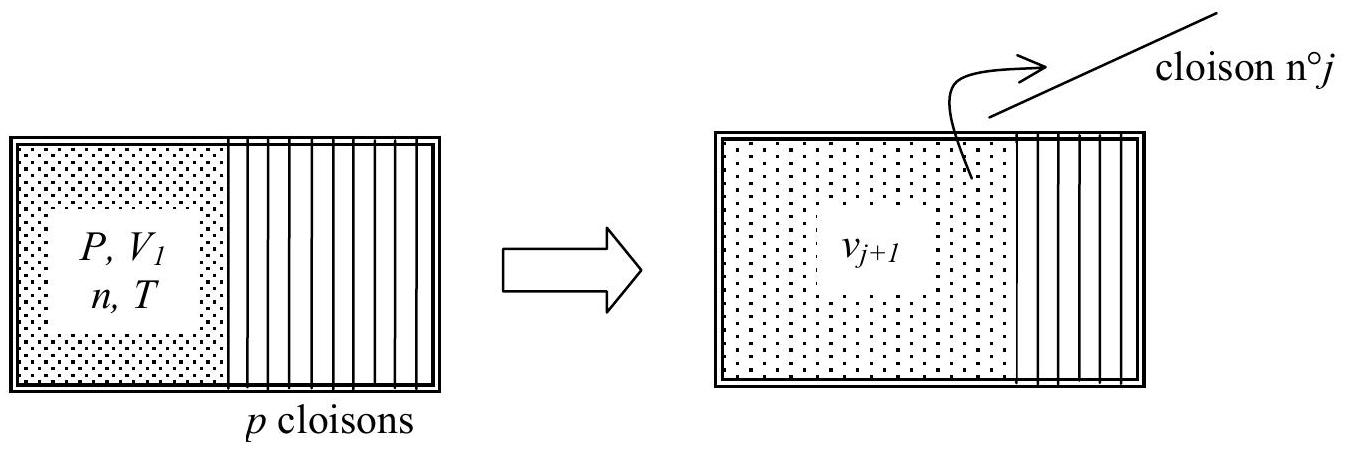
Fig. 4 : détente de Joule Gay-Lussac réalisée de façon quasi statique
