L'objet de ce problème consiste à étudier les oscillations d'un système mécanique au
voisinage d'une bifurcation (changement du nombre de positions d'équilibre, de la position
d'équilibre stable...)

On s'intéresse au système mécanique suivant: un point matériel M de masse m est fixé à l'extrémité d'un ressort de longueur à vide 1. et de constante de raideur k. La masse peut coulisser sans frottement horizontalement sur une tige (figure 1). On repère la position de la masse ni sur cette tige par l'abscisse x dont l'axe est confondu avec la tige, et dont l'origine 0 est située sur la même verticale que le point d'attache R fixe du ressort.

La tige se trouve à une distance 1 du point R :

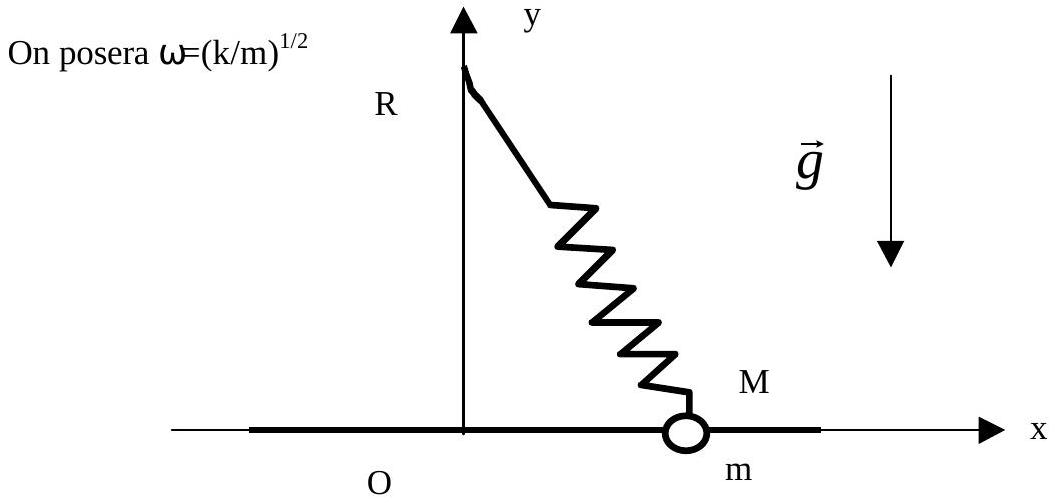
Figure 1

A. Positions d'équilibre

Initialement le point matériel M se trouve en 0 et lo. Décrire qualitativement (aucun calcul n'est demandé) le nombre de positions d'équilibre et la stabilité de celles-ci suivant qu'on rapproche la tige du point R (c'est-à -dire , ) ou qu'on éloigne la tige du point R (soit ,).
On considère maintenant (quelconque). Déterminer l'énergie potentielle élastique en fonction de et . On prendra .
Expliquer dans le cas général où l'énergie potentielle d'un point matériel de masse ni ne dépend que d'un seul paramètre (dans ce problème, il s'agit de x ), quelles sont les conditions sur en un point d'équilibre stable. On dessinera l'allure de pour un équilibre stable et un équilibre instable.
Déterminer en utilisant les questions 2 et 3 , les positions d'équilibre x , de la masse m en distinguant les cas et . Dans chaque cas, préciser si la position d'équilibre est stable ou non.
Tracer, sur un même graphe, en fonction de la distance . On précisera sur le graphe la nature de l'équilibre (stabilité ou instabilité). Pouvez-vous justifier alors le nom donné à la bifurcation (existant en ) : bifurcation fourche.
On dit également de cette bifurcation qu'elle est à symétrie brisée: justifier cette propriété.

B. Pulsation autour d'une position d'équilibre stable

On cherche maintenant à déterminer les pulsations des oscillations autour des positions d'équilibre stable.

En écrivant le principe fondamental de la dynamique appliqué au point matériel de masse ni, montrer que la pulsation s'exprime sous la forme générale:

On pourra écrire la relation fondamentale de la dynamique dans le cas général où la force dérive d'un potentiel

en développant celle-ci à l'ordre 2 en

, au voisinage proche de la position

d'équilibre.
2) Pour le système étudié, exprimer maintenant

en fonction de

et 10 . On distinguera les cas

.
3) Tracer

en fonction de 1.
4) Montrer qu'au voisinage de

, on peut écrire la pulsation sous là forme:

Déterminer les exposants, dits critiques,

ainsi que les coefficients a et

.
5) On s'intéresse au cas limite où

. On lâche la masse ni sans vitesse initiale, écartée d'une distance

.
a. Montrer graphiquement que le mouvement est périodique.
b. Par une méthode énergétique, exprimer la vitesse de la masse en fonction de

.
c. Exprimer la période des oscillations en fonction de.

et de l'intégrale

dans l'hypothèse où

est très petit devant.

.
d. Peut-on dire que cet oscillateur est harmonique?

C. Discussion

Le point matériel est également relié à un autre ressort identique au premier, fixé lui aussi sur
l'axe Oy à une distance 1 de la tige mais symétriquement à R par rapport à l'axe Ox . Qu'estce qui change par rapport à l'étude précédente?
M n'est attaché qu'à un seul ressort, mais la tige Ox n'est pas tout à fait horizontale: elle est inclinée d'un petit angle 0 . Y-a-t-il un terme nouveau dans l'énergie potentielle? Dessiner l'allure de pour dans ce cas. Quelle est la conséquence principale sur les positions d'équilibre?
Proposer une démarche expérimentale pour déterminer les exposants critiques. Leur obtention vous semble-t-elle aisée?

PROBLEME 2: OPTIQUE

On cherche dans ce problème à étudier le passage d'une source ponctuelle à une source large, et notamment le problème de la localisation des franges dans le cas de l'interféromètre de Michelson dans les deux situations: en lame d'air et en coin d'air.

Aucune connaissance sur la théorie de la localisation des franges n'est nécessaire pour faire le problème.

Partie 1: Michelson en lame d'air

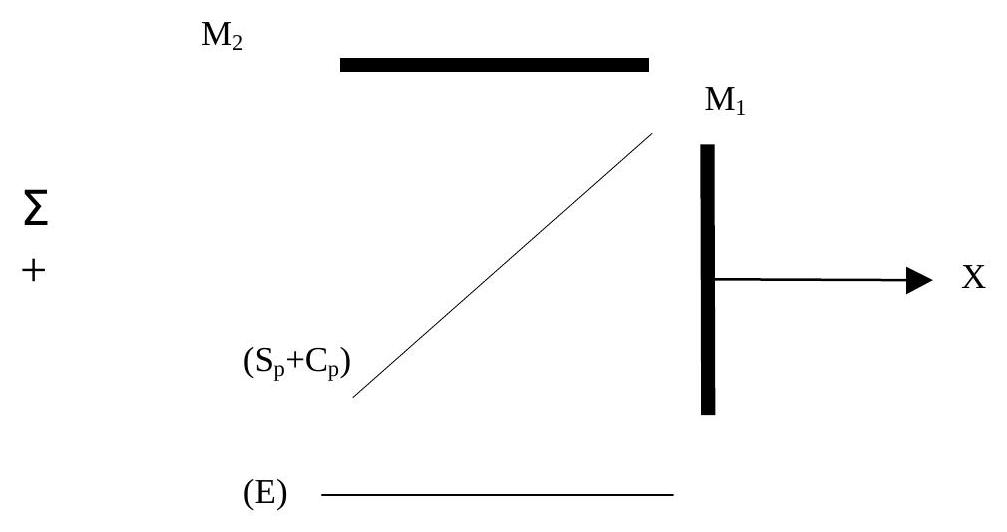
Figure 1: Interféromètre de Michelson en lame d'air

On considère un interféromètre de Michelson dont les miroirs

sont perpendiculaires. Les deux miroirs sont initialement à égale distance de 'l'ensemble séparatricecompensatrice

. L'interféromètre est éclairé par une source ponctuelle

monochromatique, de longueur d'onde

. On place un écran (E) à la "sortie" de l'interféromètre, parallèle au miroir

On déplace le miroir

d'une distance e perpendiculairement à lui-même, selon l'axe des x . (Figure 1)

a. Montrer l'équivalence du Michelson dans cette configuration avec une lame d'air (Figure 2). [Les échelles de la figure 1 et de la figure 2 ne sont pas les mêmes.]. A quoi correspondent dans le schéma équivalent ' et S ? On appelle D la distance entre et l'écran E (dont on repère la position d'un point M par l'axe OX ), et d la distance entre S et

On suppose que

sont nettement plus grandes que e.

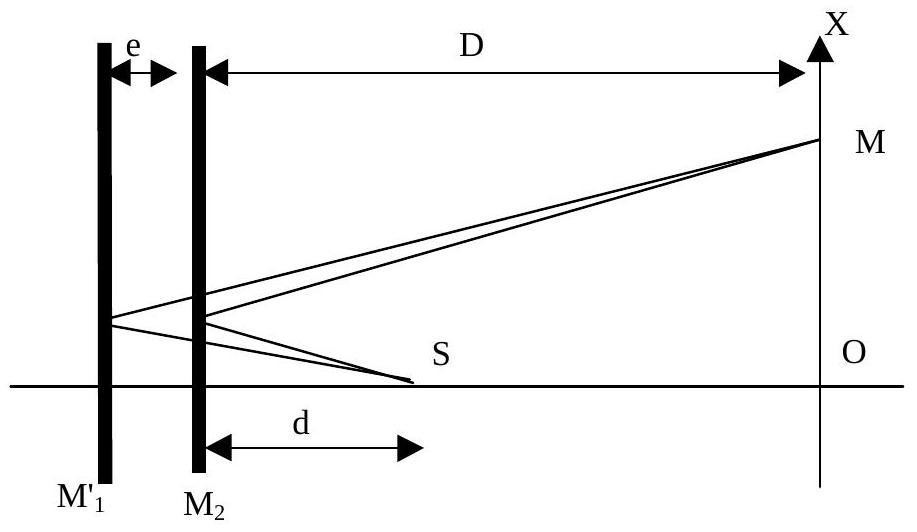
Figure 2: Equivalence en lame d'air

b. Faire un dessin de deux rayons différents issus de la source réelle

et interférant en un point M de (E) à partir de la Figure 1.

Dans la suite de cette partie, on ne raisonnera plus qu'à partir de la lame d'air.

On cherche à calculer la différence de marche entre les rayons issus de (de la Figure 2) et qui interférent en un point de (E) tel que , en se limitant aux rayons peu inclinés sur l'axe OS. Montrer que cette différence de marche est donnée par:

Justifier que les franges sont des anneaux.
3) On suppose, pour simplifier, que

où

est un entier. Qu'observe-t-on en

? Lorsque l'on s'éloigne de O , on observe une alternance d'anneaux sombres et brillants. Quel est l'ordre d'interférence p correspondant à l'anneau brillant numéro m (que l'on exprimera en fonction de

et m )?

Exprimer le rayon

de cet anneau en fonction de

, e et m . Calculer numériquement

, pour m variant de 0 à 5 (on présentera les résultats sous forme d'un tableau) pour

. Tracer

en fonction de m . Comment évolue la distance entre deux anneaux successifs?
4) On considère en plus de la source

, une autre source

' placée à une

de l'axe

au dessus ou en dessous de

' émettent de façon incohérente à la même longueur d'onde

. On cherche à savoir à quelle condition les interférences sont encore visibles et dans quelle partie de l'espace. On choisit le critère suivant (de façon un peu arbitraire): les interférences sont encore visibles si le décalage entre ces deux systèmes de franges est inférieur à

d'interfrange. Trouver une condition sur R pour que les m premiers anneaux soient visibles.
5) Montrer que si D tend vers l'infini, on peut remplacer la source ponctuelle du début par une source large (forme d'un disque de rayon

) sans changer l'allure de la figure d'interférences. Quel est l'intérêt d'utiliser une source étendue à la place d'une source ponctuelle? Comment fait-on pour observer des anneaux à l'infini? Faire un schéma en donnant un maximum d'informations sur les distances, propriétés et qualités des instruments d'optique...
6) On souhaite observer le plus grand nombre d'anneaux possible avec une source étendue: quelle condition cela impose-t-il sur l'angle maximal d'inclinaison des rayons issus de

? Comment dans la pratique réalise-t-on cette condition?
7)

Partie 2: Michelson en coin d'air

On règle maintenant l'interféromètre de Michelson, éclairé par une source ponctuelle

émettant à la longueur d'onde

, avec les miroirs

ne faisant plus un angle droit mais un angle

où

est angle très faible (Figure 3).

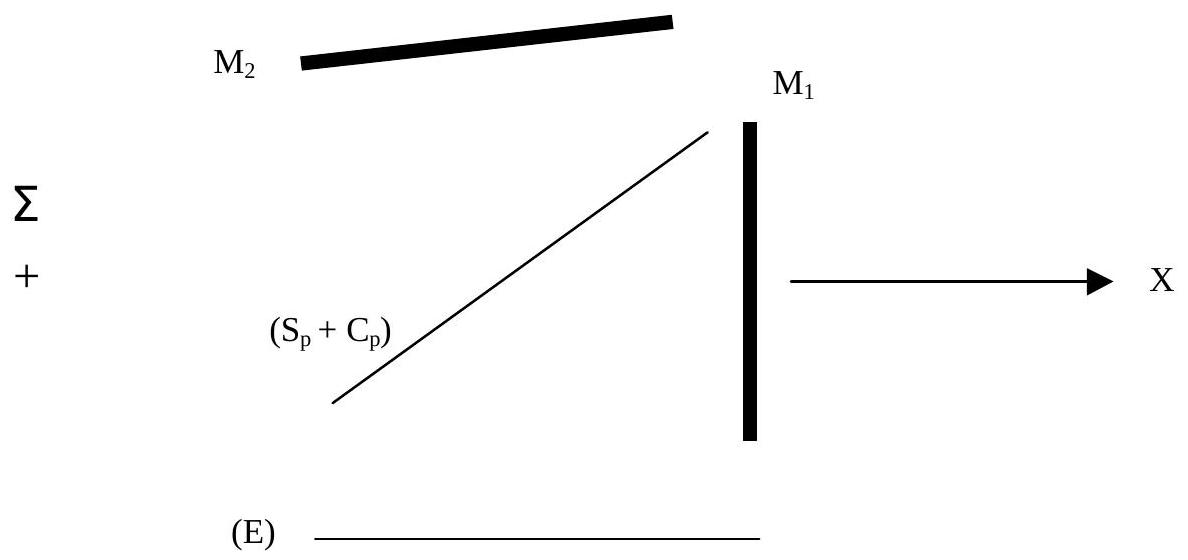
Figure 3: Interféromètre de Michelson en coin d'air

Montrer que le système considéré est équivalent à un coin d'air (Figure 4). Faire un dessin avec deux rayons issus de E interférant en un point M de l'écran (E) disposé perpendiculairement à , à partir de la Figure 3 .

Dans la suite on ne raisonnera plus que sur le coin d'air.

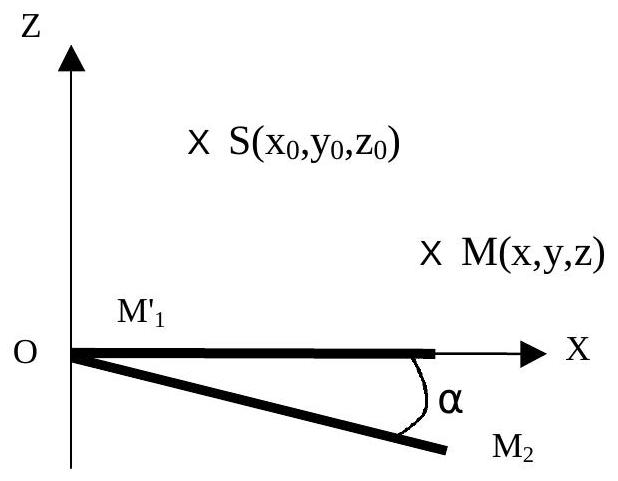
Figure 4: Coin d'air

La source

(qui a même signification que dans la partie 1) est repérée par ses coordonnées (

); le point M par ses coordonnées notées (

). Le repère Oxyz est direct.

On fera les hypothèses suivantes: (

est petit (on assimilera donc

et on ne gardera pas les termes en

d'ordre supérieur ou égal à deux), et

sont très inférieurs à

.
2) Montrer que les images

données respectivement par

ont pour coordonnées (dans le cadre de nos hypothèses):

Montrer que la différence de chemin optique entre deux rayons qui interfèrent en s'écrit:
On observe les interférences sur un écran (E) parallèle au miroir ' à la côte z . Quelle est l'allure des franges? Que vaut l'interfrange? Donner la position de la frange centrale x , définie par un ordre d'interférences nul. Dans quel cas l'interfrange est-elle indépendante de la position de l'écran? Quelle est la valeur de l'interfrange dans ce cas? Pouvait-on prévoir ce résultat?
Montrer que si l'on remplace la source ponctuelle par une fente allongée parallèle à l'arête du coin, cela ne modifie pas l'allure des franges précédentes.
On déplace maintenant cette fente-source parallèlement à elle-même, selon l'axe des x . Est-ce que le système de franges se déplace aussi? En déduire la largeur maximale que peut avoir une fente-source pour que les interférences demeurent visibles dans le plan de E en utilisant le même critère qu'à la question 4 de la partie 1 . On donnera le résultat en fonction de et .
En déduire que si (E) est placé au voisinage du coin d'air, on peut observer les franges même avec une source large.
Comment en pratique observe-t-on les interférences en coin d'air? Faire un schéma et préciser les différentes valeurs entrant en jeu.

CCINP Physique TSI 2000

ÉPREUVE SPÉCIFIQUE-FILIÈRE TSI PHYSIQUE

L'usage des calculatrices programmables et alphanumériques est autorisé sous réserve des dispositions définies dans la circulaire n' 99-018 du 01. 02.99.

PROBLEME 1: MECANIQUE