J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

CCINP Physique Chimie PSI 2014

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ccinp
🔗 Explorer
Banque
CCINP
Année
2014
Filière
PSI
Matière
Physique Chimie
CCINP PSICCINP 2014PSI Physique ChimiePhysique Chimie 2014
2025_09_04_1f11962e21dfafa8ce72g

EPREUVE SPECIFIQUE - FILIERE PSI

PHYSIQUE 2

Durée : 4 heures
N.B. : Le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.
Les calculatrices sont autorisées

PROBLEME DE PHYSIQUE CHIMIE

CUIVRE ET SUPRACONDUCTIVITE

Une annexe donnant le diagramme E-pH du cuivre, des données et un formulaire global se trouve en fin d'énoncé en pages 13 et 14.

PARTIE CHIMIE

A) Etude cristallographique du cuivre :

Le cuivre comme de nombreux métaux cristallise suivant la structure cubique à face centrée.
  1. Représenter en perspective l'allure d'une maille élémentaire.
  2. Définir en une phrase le terme de coordinence. Préciser sa valeur dans le cadre de la structure étudiée.
  3. Comment s 'effectue le contact entre les atomes? En déduire la relation entre le paramètre de maille a et le rayon atomique R .
  4. Combien y a-t-il d'atomes par maille ?
  5. Définir la compacité C , donner son expression littérale puis l'évaluer numériquement. Est-ce une structure compacte ?
  6. Soient M la masse molaire du cuivre, R son rayon atomique, le nombre d'Avogadro et la masse volumique du cuivre, déterminer la relation entre et .
  7. Application numérique : évaluer M . En déduire la période de la classification des éléments à laquelle appartient le cuivre.

B) Diagramme E-pH du cuivre :

Les espèces prises en compte sont : et . On ne tient donc pas compte du degré d'oxydation + III.
On supposera que la concentration totale en espèces dissoutes vaut .
8) Classer les espèces par degré commun d'oxydation et déterminer pour chaque degré d'oxydation les domaines de prédominance de chacune des espèces en fonction du pH .

Etude du couple :

L'allure du diagramme du couple (figure 1) est le suivant :
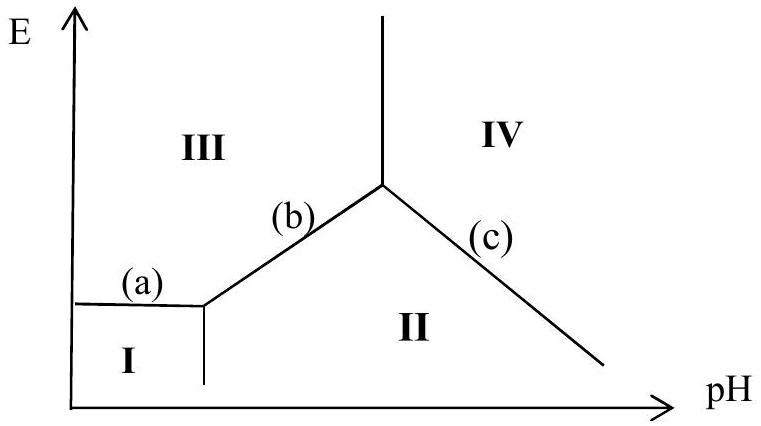
Figure 1 : diagramme E-pH du couple
  1. Reproduire sur votre copie l'allure de ce diagramme E-pH en y plaçant les espèces numérotées de I à IV.
  2. Quelle est la valeur du potentiel du segment horizontal (a) ?
  3. Déterminer la pente puis l'équation complète du second segment (b).
On admettra que la pente du troisième segment (c) est de - unité de pH .
Etude du couple :
L'allure du diagramme du couple (figure 2) est le suivant :
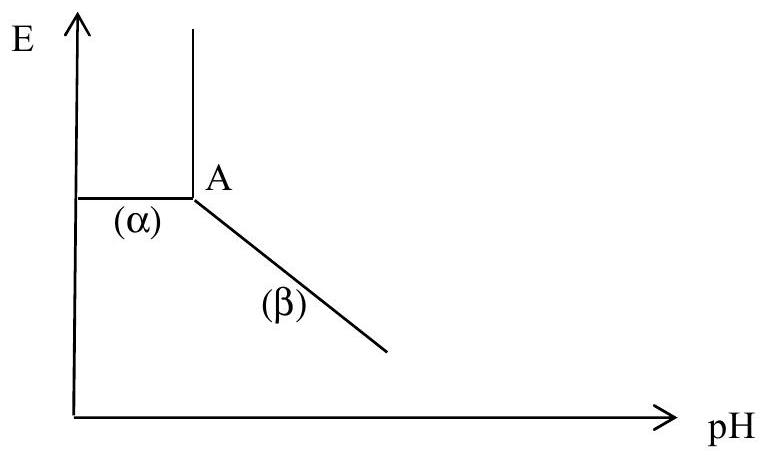
Figure 2 : diagramme E-pH du couple
  1. Déterminer les coordonnées du point ainsi que la pente du second segment ( ). En déduire l'équation complète du segment ( ).
Diagramme E-pH provisoire :
13) Superposer les deux diagrammes précédents. Commenter. Préciser le pH d'intersection des segments (b) et ( ).

Diagramme du cuivre :

  1. Déterminer le potentiel standard du couple .
  2. Donner l'équation du potentiel correspondant à la frontière pour . Est-il nécessaire d'étudier ce couple pour ? Justifier.
  3. Sur votre copie, reproduire le diagramme du cuivre fourni en annexe. Compléter la frontière manquante et placer les différentes espèces du cuivre. La représentation doit être claire et soignée car elle servira à nouveau par la suite.
  4. On considère la réaction chimique : . Comment nomme-t-on ce type de réaction ? Evaluer sa constante d'équilibre .

C) Diagramme E-pH de l'eau ou de ses ions :

L'eau (ou ses ions) peut agir comme oxydant ou comme réducteur.
Dans cette partie, on supposera les pressions égales à la pression standard, soit , avec bar ou .
18) Ecrire les deux demi-réactions d'oxydoréduction dans lesquelles interviennent les couples de l'eau. En déduire les deux équations des deux droites , figurant dans le diagramme E-pH de l'eau.
19) Superposer le diagramme de l'eau sur le diagramme du cuivre tracé à la question 16).
20) Pourquoi le cuivre est-il qualifié de métal noble ? Justifier son utilisation dans la marine antique (scaphandre, poulie...). Connaissez-vous d'autres métaux nobles ? En citer deux.

D) Lixiviation du cuivre et préparation d'une solution de cuivre II :

  1. Définir en une phrase le terme de lixiviation acide.
  2. On considère la réaction chimique: .
Evaluer la constante d'équilibre de cette réaction.
23) A partir de quelle valeur de pH faut-il travailler pour obtenir une solution de concentration minimale égale à de cuivre (II) dissous ?
On désire réaliser une solution d'acide sulfurique satisfaisant cette condition.
24) En remarquant que la acidité est forte (réaction totale), que la acidité est faible et, en ne considérant que la (ou les) réaction(s) prépondérante(s), établir une relation entre la concentration C d'une solution d'acide sulfurique et la concentration en ions .
25) Quelle est la valeur minimale de C pour que le pH soit inférieur à 4 ?

E) Détermination expérimentale de la composition d'une céramique supraconductrice :

Les céramiques supraconductrices de formule générale présentent un état supraconducteur pour des températures supérieures à celle de l'azote liquide sous la pression atmosphérique et sont ainsi qualifiées de supraconducteurs à haute température critique. Elles contiennent des anions oxydes, des cations et , ainsi que des ions et en proportions variables.
La détermination expérimentale de leur composition peut s'effectuer en réalisant les deux expériences suivantes.

Expérience 1:

  • une petite quantité de solide (de l'ordre de ) est dissoute, à chaud, dans 20 mL d'une solution d'acide chlorhydrique à ;
  • on ajoute ensuite un excès d'iodure de potassium. On observe alors la formation d'un précipité d'iodure cuivreux CuI et l'apparition de diiode ;
  • le dosage du diiode formé nécessite un volume é de de thiosulfate de sodium à .

Expérience 2:

  • la même quantité de solide est maintenant dissoute, à froid, dans 20 mL d'une solution d'acide chlorhydrique à ;
  • on ajoute ensuite un excès d'iodure de potassium. On observe alors la formation d'un précipité d'iodure cuivreux CuI et l'apparition de diiode ;
  • le dosage du diiode formé nécessite, cette fois, un volume é de de thiosulfate de sodium à .
  1. En s'appuyant sur l'échelle des potentiels standards et l'absence d'ions iodure, quelle réaction d'oxydo-réduction s'attend-on à observer pour les ions en solution aqueuse à ?
  2. Cette réaction n'est pas observée à froid. Proposer une explication.
  3. a) Après dissolution à chaud de la céramique supraconductrice dans la solution d'acide chlorhydrique, sous quel(s) forme(s) ionique(s) se trouve le cuivre dans l'expérience 1 ?
    b) Après dissolution à froid de la céramique supraconductrice dans la solution d'acide chlorhydrique, sous quel(s) forme(s) ionique(s) se trouve le cuivre dans l'expérience 2 ?
  4. Ecrire la (ou les) réaction(s) chimique(s) qui aboutit(ssent) à la formation du précipité CuI.
  5. Ecrire la réaction de dosage du diiode par le thiosulfate.
  6. On note respectivement x et y les nombres de moles initiales de et de contenues dans la pastille supraconductrice solide qui a été dissoute.
    Déterminer une relation entre é et é. Evaluer le rapport .
  7. Déterminer la valeur de n dans la formule brute de la céramique supraconductrice.

PARTIE PHYSIQUE

F) Création d'un champ magnétique intense à l'aide d'un solénoïde :

L'imagerie médicale a besoin de champ magnétique intense, permanent et uniforme. On se propose ici de dimensionner une bobine dans laquelle règne un champ magnétique de 2 T .

Résistance électrique d'un conducteur ohmique :

On considère un conducteur ohmique (figure 3), de conductivité électrique , de section S , de longueur , parcouru par un courant électrique continu uniformément réparti de densité : .
Figure 3 : conducteur ohmique
  1. Exprimer, en fonction de et , le champ électrique qui règne à l'intérieur de ce conducteur.
  2. Donner, en fonction de , et des caractéristiques géométriques de ce conducteur, les expressions du courant électrique I traversant ce conducteur et de la différence de potentiel U aux bornes de ce conducteur.
  3. En déduire, en fonction de et des caractéristiques géométriques de ce conducteur, la résistance électrique de ce conducteur.

Caractéristiques de la bobine à température ambiante :

On suppose ici que la bobine est maintenue à température ambiante .
La bobine (figure 4, page 7) est assimilée à un solénoïde d'axe Oz , de longueur L , de rayon moyen avec . Les effets de bords sont négligés, le solénoïde est donc considéré comme infini. Il est constitué de spires jointives d'un fil de cuivre de diamètre d et de conductivité électrique . Chaque spire est parcourue par un courant I. Il comporte p couches de bobinage superposées.
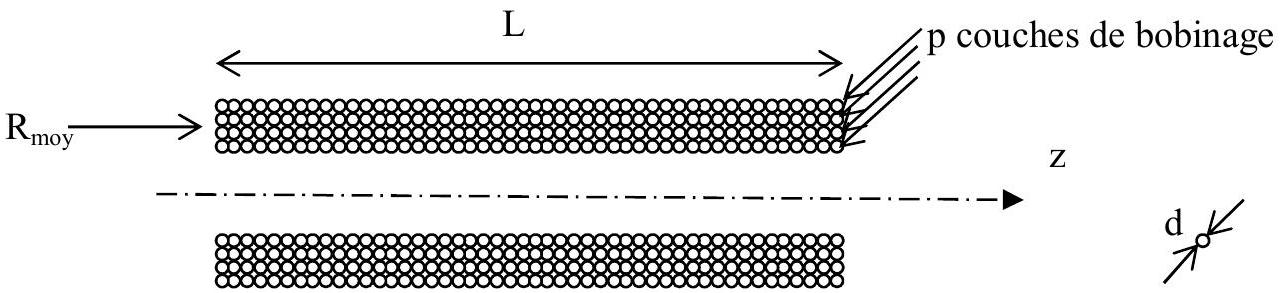
Figure 4 : bobine
  1. a) Sur une seule couche de bobinage, combien y a-t-il de spires jointives par unité de longueur de solénoïde ?
    b) Combien de spires par unité de longueur comporte ce solénoïde ?
  2. a) Donner, en fonction de , I et , l'expression du champ magnétique créé à l'intérieur du solénoïde.
    b) Application numérique : . Déterminer p .
  3. a) En assimilant le rayon de chaque spire au rayon moyen, , exprimer la longueur, , de fil nécessaire à la réalisation de cette bobine en fonction de et L .
    b) Application numérique : et . Evaluer .
  4. a) Exprimer en fonction de , de et de d la résistance électrique é de la bobine.
    b) Application numérique : évaluer la puissance , dissipée par effet Joule dans la bobine. Commenter.

Caractéristiques de la bobine refroidie à 77 K :

On suppose ici que la bobine est maintenue à la température de 77 K .
Pour diminuer la puissance dissipée, on peut envisager de refroidir le conducteur en cuivre par l'intermédiaire d'un bain d'azote liquide à 77 K . On peut alors imposer dans un conducteur de cuivre, de même diamètre , un courant plus important . On réduit ainsi le nombre de spires de la bobine et donc sa résistance électrique et son rayon moyen.
40) a) Quel est alors le nombre de couches de bobinage, p ', à superposer pour obtenir un champ magnétique de 2 T ?
b) En assimilant le rayon de chaque spire au nouveau rayon moyen, , évaluer la nouvelle puissance dissipée par effet Joule, , dans la bobine.
Compte-tenu du coût de la réfrigération de la bobine à 77 K , il faut tenir compte de l'efficacité de la machine thermique assurant le maintien de cette basse température.
41) On considère une machine frigorifique cyclique et réversible qui assure, par l'intermédiaire d'un fluide caloporteur, les transferts thermiques entre deux sources de températures constantes et .
a) En effectuant un bilan énergétique et un bilan entropique sur un système bien défini, exprimer l'efficacité, e é, de cette machine en fonction de et de .
b) Application numérique : et . Evaluer é.
42) Evaluer la puissance , minimale, nécessaire pour absorber la puissance , dissipée dans la bobine en cuivre refroidi. Commenter.

G) Puissance dissipée dans le supraconducteur lors des régimes transitoires :

Si les supraconducteurs sont dépourvus de pertes en régime continu, il n'en est pas de même en régime variable. Pour les bobines alimentées en courant continu, ces pertes ont lieu lors des deux régimes transitoires qui correspondent en début d'utilisation de la bobine à l'installation du courant dans le conducteur, puis en fin d'utilisation de la bobine, lors de la redescente à zéro de ce courant.
On se propose ici de déterminer l'ordre de grandeur de la puissance dissipée par unité de longueur de conducteur, lors de la première montée du courant, dans une situation dite de champ propre, c'est-à-dire lorsqu'une portion de conducteur est soumise aux variations temporelles du champ magnétique qu'il crée sur lui-même.
On assimile le supraconducteur (figure 5) à un fil rectiligne infini suivant l'axe Oz, de rayon R. On adopte les coordonnées cylindriques.
Figure 5 : supraconducteur
Compte-tenu des invariances du problème, la densité volumique de courant, notée , dans le supraconducteur ne dépend que de r et est portée par le vecteur . On a : . Pour un courant de transport I donné, la densité de courant n'est pas uniforme dans le supraconducteur, son amplitude vaut ou 0 , où est une constante. Ce courant se distribue de façon à protéger le centre du supraconducteur de toute variation de champ magnétique.
43) Déterminer en fonction de et de la valeur maximale , dite valeur critique du courant de transport de ce conducteur.

Etude de la première montée du courant dans le supraconducteur :

On s'intéresse ici à la première montée du courant dans le supraconducteur.
On suppose que cette première montée s'effectue, pendant une durée , suivant une consigne en rampe de sorte que: , où est la valeur finale du courant dans le supraconducteur.
Ce courant se distribue de façon à protéger le centre du supraconducteur de toute variation de champ magnétique, de sorte qu'il se répartit, à un instant t de cette première étape, à la périphérie du supraconducteur dans la zone : (figure 6).
On a : pour et pour .
Figure 6 : répartition du courant dans le supraconducteur
  1. On définit par le taux d'utilisation du supraconducteur. Exprimer u en fonction de , et .
  2. a) Déterminer la relation qui existe entre et R .
    b) En déduire l'expression de en fonction de et .
    c) Exprimer en fonction de et .
  3. a) A l'aide de propriétés de symétrie et d'invariance, préciser de quelle(s) variable(s) de l'espace dépend le champ magnétique dans le supraconducteur et par quel(s) vecteur(s) de base il est porté.
    b) Par application du théorème d'Ampère, dans l'approximation des régimes quasistationnaires, sur un contour que l'on précisera, déterminer à l'instant t le champ magnétique dans la zone : .
    c) De même, déterminer en fonction de , et , le champ magnétique dans la zone : .
    d) Tracer l'allure de la fonction à un instant t , pour .
  4. a) Rappeler l'équation de Maxwell-Faraday. Donner le nom du phénomène physique régi par cette loi. Historiquement, à quel siècle a-t-elle été découverte ?
Pour les questions 47) b) et 47) c), on admettra que toute contribution du champ électrique, qui ne dépend que de l'espace ou que du temps, sera assimilée à la fonction nulle.
b) Que vaut le champ électrique pour ?
c) En remarquant que le champ électrique est continu en et qu'il peut s'écrire sous la forme : , montrer que pour .
48) Quelle est l'unité de ? Proposer, en quelques lignes, un protocole permettant de visualiser expérimentalement le champ électrique sur un écran d'oscilloscope ou d'ordinateur.
49) Donner l'expression de la densité volumique locale et instantanée de puissance dissipée dans le supraconducteur, notée :
a) dans la zone : ,
b) dans la zone : .
50) Par intégration sur l'espace, en déduire, en fonction de , , u et , l'expression de la puissance é dissipée dans une longueur de supraconducteur à l'instant t lors de la première montée du courant.
51) a) Par intégration sur le temps, déterminer l'énergie Q dissipée lors de la première montée du courant dans un supraconducteur de longueur en fonction de et u .
b) Est-il utile d'augmenter la durée T d'établissement de ce courant pour réduire l'énergie dissipée dans le supraconducteur?
52) La machine thermique qui assure le refroidissement du supraconducteur à a une efficacité de .
On donne et . Evaluer l'énergie consommée par le réfrigérateur devant absorber l'énergie Q dissipée lors de la première montée du courant. Commenter.

H) Stabilité thermique des filaments supraconducteurs :

Equation de la diffusion thermique en régime permanent:
On considère un conducteur thermique cylindrique (figure 7, page 11) supposé infini, siège de conduction thermique longitudinale suivant . On ne considère ici que le régime permanent. La température est supposée uniforme sur toute section droite S du conducteur. On note k sa conductivité thermique.
Figure 7 : conducteur thermique
  1. Rappeler la loi de Fourier et préciser l'unité du vecteur qui intervient.
  2. En raisonnant sur une tranche de conducteur comprise entre les abscisses et , sachant que notre conducteur thermique est le siège d'une source de chaleur interne de densité volumique de puissance , retrouver l'équation de la diffusion thermique en régime permanent.

Application au supraconducteur :

On rappelle qu'un matériau supraconducteur est effectivement dans l'état supraconducteur si sa température est inférieure à une température critique notée .
On considère ici que notre conducteur cylindrique de rayon R est traversé par un courant électrique uniformément réparti de densité .
De plus, les phénomènes de conduction thermique longitudinale étant bien plus efficaces que les échanges conducto-convectifs de surface, on suppose qu'il n'y a pas d'échange thermique en , entre le conducteur et le bain d'hélium dans lequel il trempe (figure 8).
Figure 8 : conducteur thermique et bain d'hélium
Au sein d'un supraconducteur, une perturbation peut faire transiter une zone supraconductrice en une zone résistive, dite normale. Cette zone normale peut parfois se résorber d'elle-même en se refroidissant par conduction thermique avec ses zones voisines supraconductrices. On se propose de déterminer ici l'ordre de grandeur de la longueur maximale, , capable de se résorber d'elle-même.
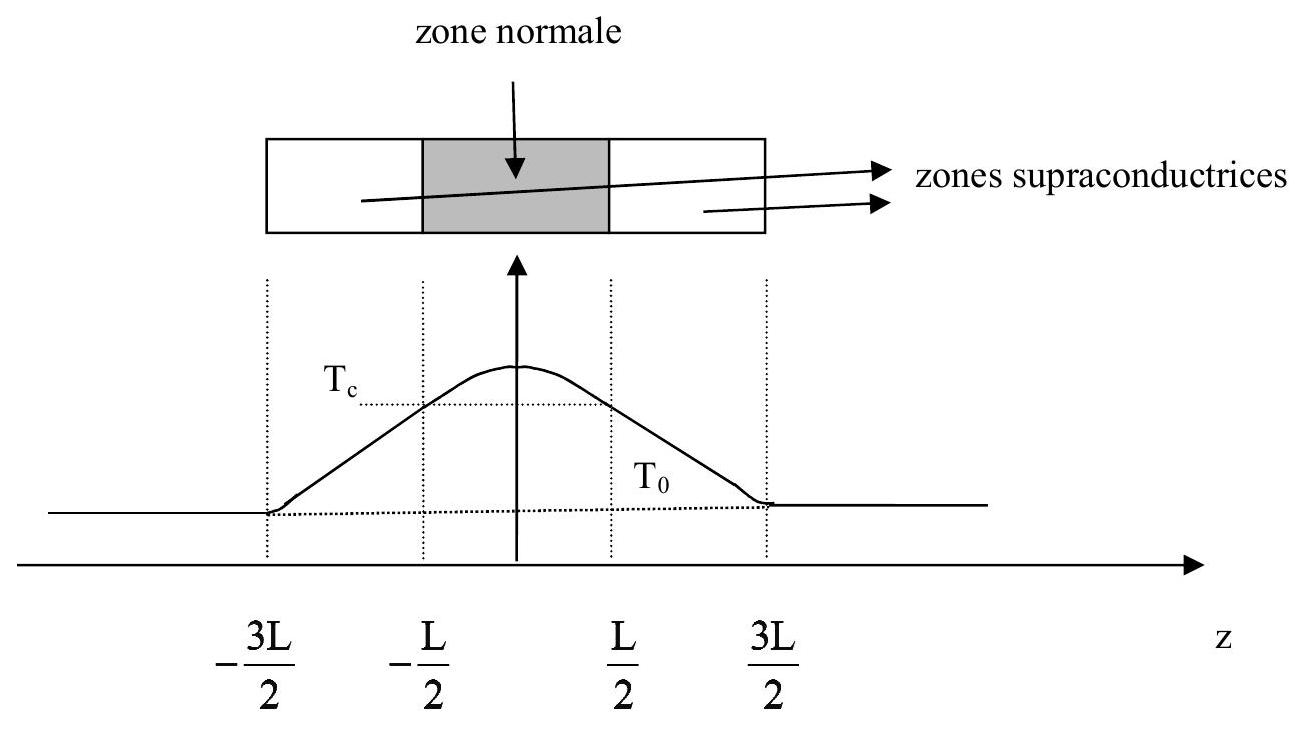
Sur la figure 9, ci-dessous, on a représenté une zone normale ( ), de longueur L , dont on note sa résistivité électrique. Le reste du conducteur est à l'état supraconducteur et est donc dépourvu de toute résistivité électrique. On suppose que le profil de température de part et d'autre de cette zone normale est le suivant :
Figure 9 : profil de température
55)a) Quel phénomène est à l'origine d'une dissipation de puissance dans la zone normale ?
b) Donner l'expression de la densité volumique de puissance , dissipée dans cette zone normale en fonction de et de .
56) Justifier l'allure générale du profil de température pour .
57) Exprimer, en fonction de , L et S , la puissance dissipée dans la zone normale.
58) a) Donner, en fonction de et , l'expression du vecteur densité de courant thermique dans la zone supraconductrice .
b) Donner, en fonction de et , l'expression du vecteur densité de courant thermique dans la zone supraconductrice .
59) En déduire la puissance thermique sortant de la zone normale en fonction de et S .
60) a) Exprimer, en fonction de et , la longueur maximale d'une zone normale capable de se résorber d'elle-même.
b) Application numérique : et . Evaluer .
c) Pourquoi les conducteurs supraconducteurs sont-ils constitués d'un grand nombre de filaments submicroniques?

ANNEXE

Diagramme E-pH du cuivre.

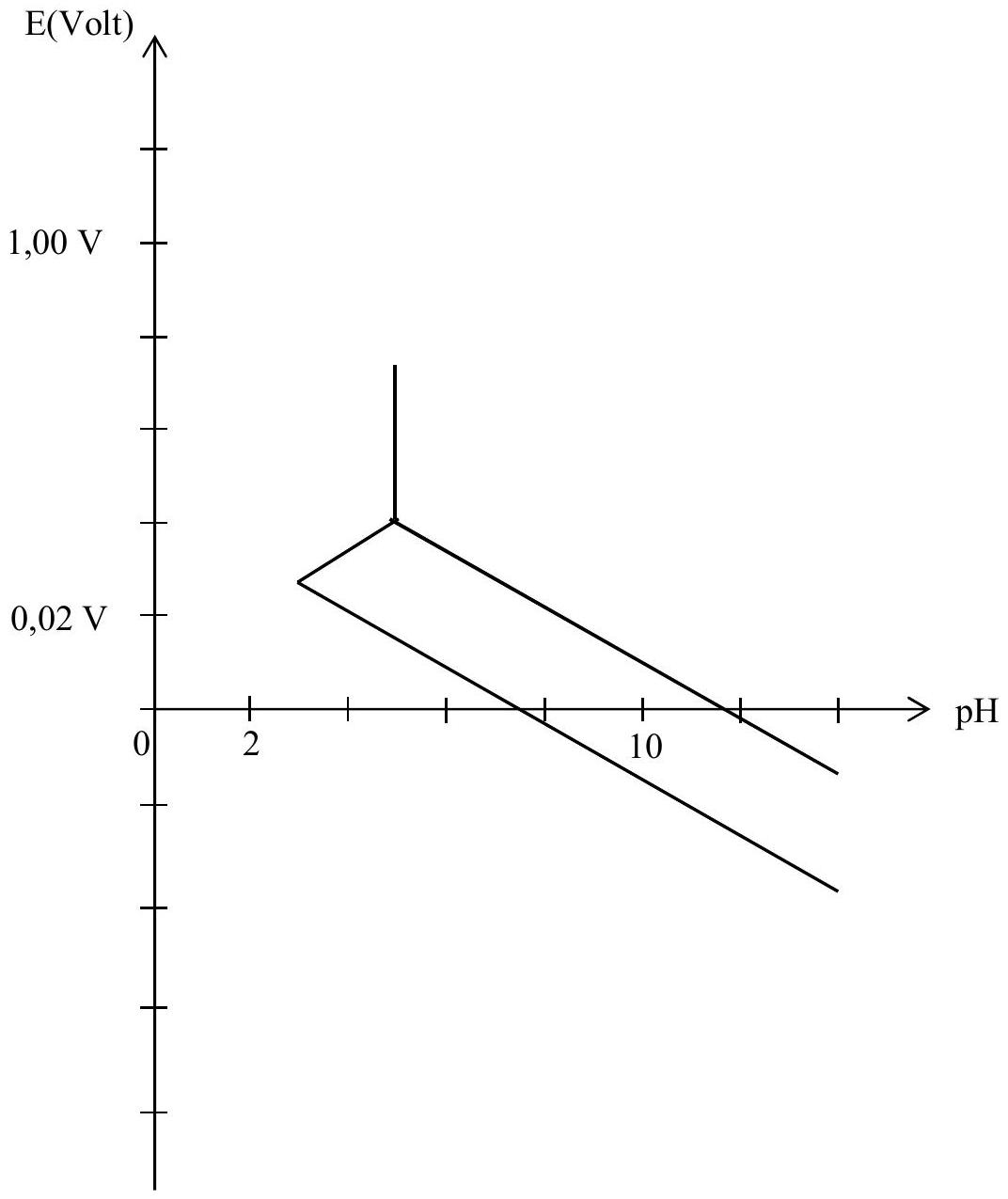
Données :

Constante d'Avogadro: .
Rayon atomique du cuivre:
Densité du cuivre : .
Potentiels standards à 298 K :
Produits de solubilité :
L'acide sulfurique ( ) est un diacide dont la acidité est forte et la acidité est faible. On donne .
Produit ionique de l'eau: .

Constantes physiques :

Conductivité électrique du cuivre :

Formulaire mathématique :

Fonction : Primitive :

Opérateurs vectoriels en coordonnées cylindriques :

Fin de l'énoncé

CCINP Physique Chimie PSI 2014 - Version Web LaTeX | WikiPrépa | WikiPrépa