l'impédance entre G et S est considérée comme infinie
entre les bornes et , la source de courant délivre un courant d'intensité proportionnelle à la différence de potentiel (on note s le facteur de proportionnalité ou transconductance, généralement exprimée en milliampères par volt).

Dans ce qui suit, on ne s'intéressera qu'au fonctionnement en régime variable.
De plus, dans les domaines de fréquence envisagés, les condensateurs

peuvent être assimilés à des courts-circuits.

On admettra que, dans ces conditions, l'amplificateur peut être représenté par le schéma très simple de la figure 3.

figure 3

figure 4

1.1.1. Montrer que l'amplificateur de la figure 3 peut aussi être représenté par le schéma de la figure 4. Donner les expressions de

(résistance de sortie) et du coefficient A (amplification) caractérisant la source de tension (attention à l'orientation).
1.1.2. On connecte un appareil de résistance d'entrée

à la sortie de l'amplificateur (entre les bornes

. Que devient le rapport

1.2. Oscillateur Colpitts à transistor

On complète le montage amplificateur de la figure 4 avec deux condensateurs de capacité C et une inductance pure L et on connecte les bornes Q et E (figure 5).

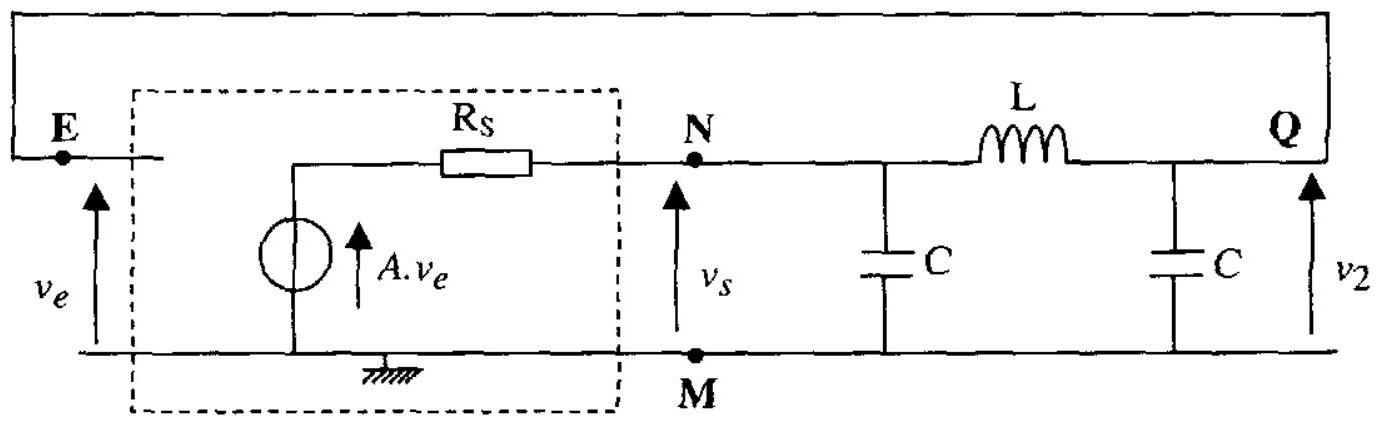
figure 5

1.2.1. Montrer que le montage peut être modélisé par le schéma de la figure 6 où:

A est le paramètre de l'amplificateur (c'est le coefficient A de la source de tension de la figure 4)

une fonction de transfert que l'on exprimera dans le formalisme de Laplace sous la forme:

(

désigne la variable de Laplace;

sont des coefficients dont on donnera l'expression en fonction de

et C

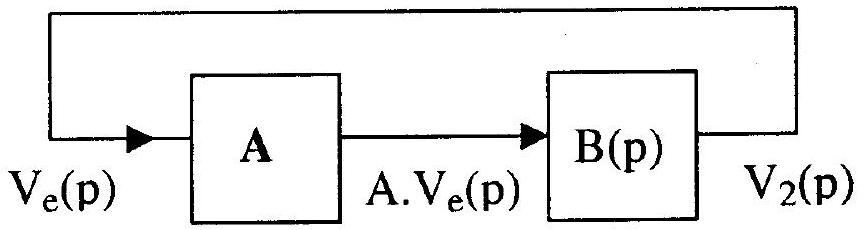
figure 6

1.2.2. En déduire que, pour assurer le fonctionnement du montage en régime sinusoïdal permanent de pulsation

, la tension ve prenant des valeurs non nulles en l'absence de tout générateur de tension sinusoïdale extérieur (fonctionnement en oscillateur quasi-sinusoïdal), il faut imposer deux conditions:

la fréquence doit avoir une valeur (à déterminer)
le paramètre A doit avoir une valeur particulière (à déterminer).
1.2.3. On admet que le montage est un oscillateur quasi-sinusoïdal de fréquence (déterminée à la question précédente).
a) Comment faire pour assurer le démarrage des oscillations (réponse qualitative sur quelques lignes) ?
b) Il y a dissipation d'énergie par effet Joule dans les différentes résistances présentes dans le montage et pourtant on n'observe pas d'amortissement des oscillations. Qui donc fournit cette énergie ?
c) On utilise des condensateurs dont la capacité est connue à près et une inductance mH évaluée à près. Calculer la fréquence d'oscillation et l'incertitude relative sur cette fréquence.
1.2.4. Quel montage simple à amplificateur opérationnel pourrait remplir la fonction amplification du bloc A de la figure 6 ? Représenter ce montage.
1.2.5. Pour obtenir des oscillateurs de fréquence élevée (plusieurs dizaines de mégahertz) avec une grande précision sur la fréquence d'oscillation (moins de 1 pour 1000), on utilise encore le montage de la figure 5 mais l'inductance est alors remplacée par un quartz piézo-électrique.

Peut-on encore employer le montage amplificateur à amplificateur opérationnel de la question précédente ? Justifier votre réponse.

DEUXIEME PARTIE

TRACE DE LA CARACTERISTIQUE D'UNE DIODE ALIMENTATION A DECOUPAGE

On quitte le domaine des faibles puissances pour s'intéresser aux applications des diodes et des transistors de puissance dans la conversion électronique de puissance.

Dans cette deuxième partie, le transistor est utilisé comme un interrupteur. Sa caractéristique courant-tension a alors la forme rappelée sur la figure 7.

Figure 7

2.1. Tracé de la caractéristique d'une diode

2.1.1. A titre de rappel, tracer l'allure de la caractéristique courant-tension

d'une diode supposée idéale (on rappellera les orientations choisies pour le courant d'intensité i et la tension

).
2.1.2. On veut tracer la caractéristique d'une diode sur l'écran d'un oscilloscope. Pour cela, on réalise le montage de la figure 8.

figure 8

Les données expérimentales sont les suivantes :

l'oscilloscope comporte deux voies (nommées X et Y ) ; les masses de ces deux voies sont toutes les deux reliées au même potentiel, celui de la « Terre» du laboratoire
l'oscilloscope est utilisé en mode XY
le générateur de fonctions est utilisé en mode sinusoïdal, la fréquence restant très basse ( 30 Hz environ). La masse de ce générateur est également reliée à la Terre du laboratoire
le transformateur est un transformateur d'isolement ( et ont mêmes valeurs efficaces)
a) Indiquer, par un schéma clair, la façon dont on doit brancher les deux voies de l'oscilloscope pour obtenir la caractéristique courant-tension sur l'écran de l'oscilloscope (courant selon l'axe vertical Y et tension suivant X).
b) Quel est le rôle du transformateur d'isolement ?
c) On considère que s'écrit

En supposant la diode idéale, tracer en les justifiant succinctement :

l'allure de , tension aux bornes de la diode
l'allure de , tension aux bornes de la résistance .
d) L' expérimentateur veut maintenant faire une mesure en régime continu. Sans changer le montage, il règle le générateur de fonctions en mode continu : constante . On suppose toujours la diode idéale. Que vaut alors le courant à travers la résistance ?
2.2. Alimentation à découpage

Dans cette partie 2.2., on ne s'intéresse qu'au fonctionnement périodique (on nomme T la période).
La structure envisagée correspond à celle des alimentations dites à découpage (figure 9).
La séquence de commande des interrupteurs est la suivante :

, K fermé, K' ouvert
ouvert, K ' fermé.

figure 9

On considère connus :

On suppose dans un premier temps que l'association R//C entourée en pointillés se comporte comme une source de tension

On se place dans l'hypothèse où le courant dans la bobine d'inductance

ne s'annule jamais.
2.2.1. Déterminer les expressions de

, intensités des courants dans la bobine

et les interrupteurs

', sur une période (on note

les valeurs minimale et maximale de

).
2.2.2. Représenter

.
2.2.3. Déterminer, en fonction de E et

, la valeur de

.
2.2.4. On règle

à la valeur

. La puissance moyenne fournie par la source de tension E est alors

On accepte une «ondulation

maximale

pour cette valeur de

.
a) Déterminer la valeur minimale de l'inductance L .
b) Pour la valeur de

trouvée à la question a) précédente, déterminer les valeurs minimale

et maximale

.
2.2.5. Choix et caractéristiques des interrupteurs
a) Tracer les portions de la caractéristique courant-tension décrites par chaque interrupteur sur les intervalles

d'une part et

d'autre part.
b) En déduire les fonctions de commutation, transistor ou diode, utilisables pour K et K ' (les interrupteurs sont supposés idéaux).
c) Que vaut la valeur moyenne

de la tension

aux bornes de K ?
2.2.6. On se place à nouveau dans les conditions du 2.2.4. :

En réalité, la tension U aux bornes de l'association R//C n'est pas constante : c'est une fonction périodique qui présente une légère ondulation. On suppose que cela ne modifie pratique ment pas

', qui conservent les mêmes formes que précédemment.
a) Déterminer, littéralement et numériquement, les intensités moyennes

des courants dans la charge R et dans le condensateur C en fonction de

et E .
b) Déterminer numériquement les valeurs moyennes

des puissances dissipées dans R et dans C .

TROISIEME PARTIE

ETUDE SIMPLIFIEE D'UN DISSIPATEUR THERMIQUE POUR TRANSISTOR

On ne peut pas toujours limiter la puissance dissipée dans un transistor. Pour pouvoir dissip er une puissance beaucoup plus élevée en limitant la température du composant, on monte le boîtier de certains transistors sur un dissipateur de chaleur (figure 10).

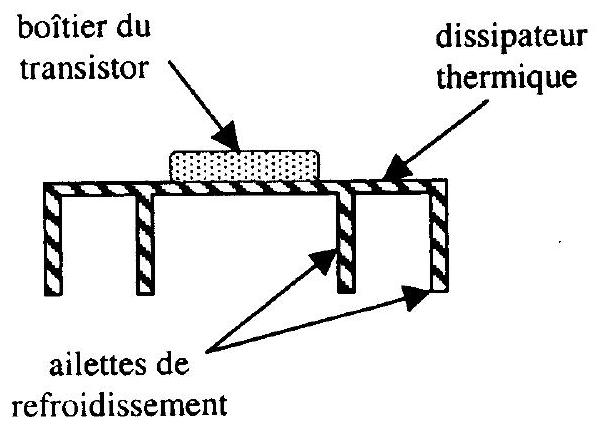
figure 10

figure 11

.Ce dissipateur est muni d'ailettes de refroidissement dont on se propose d'étudier l'intérêt.
Une ailette de refroidissement en aluminium de conductivité thermique

est fixée à un corps dont la température est

constante et baigne dans l'air ambiant dont la température est constante et vaut

.
Le corps à la température

occupe le demi-espace

.
L'ailette est de forme parallélépipédique (figure 11), d'épaisseur e

, de largeur a

et de longueur I =2 cm.

On fait les hypothèses suivantes :

le régime étudié est stationnaire
la température d'un point de l'ailette n'est fonction que de x : elle sera donc notée
a est très grand devant e (cf. valeurs numériques)
la puissance thermique cédée à l'air extérieur par la surface latérale dS d'un élément de longueur dx (échanges conducto-convectifs) est :
avec
où est un coefficient constant : S.I. (S.I. signifie : dans le système international).
Remarque: La question 3.9. peut être traitée indépendamment des questions précédentes.
3.1. Donner la loi de Fourier.
3.2. Quelle est la signification physique de cette loi ?
3.3. Quelle est l' unité du coefficient ?
3.4. Montrer que l'équation différentielle vérifiée par la température de l'ailette peut se mettre sous la forme :

où L est une longueur caractéristique que l'on exprimera en fonction de

, h et e.
3.5. Calculer la valeur numérique de L .
3.6. Justifier les deux conditions aux limites suivantes vérifiées par

.
3.7. En déduire la loi

en fonction de x .
3.8. Montrer que compte-tenu de la longueur de l'ailette (

), on peut supposer que la température de l'ailette est approximativement constante et égale à

: on montrera que la valeur absolue de

est voisine de

.
3.9. On considère que la température de l' ailette est effectivement constante et égale à

3.9.1. Donner l'expression de la puissance thermique P échangée entre l'ailette et l'air ambiant.
3.9.2. Déterminer la puissance thermique P ' échangée entre le corps à la température

et l'air ambiant par la surface d'aire

a.e en l'absence d'ailette ( S ' est la surface de base de l'ailette en

).
3.9.3. En déduire l'expression de l'efficacité

' de l'ailette.

Calculer sa valeur.

PROBLÈME DE CHIMIE

LES PROCÉDÉS CHIMIQUES DANS L'INDUSTRIE DE LA MICROÉLECTRONIQUE

Le problème proposé s'articule autour de quelques opérations chimiques de la fabrication des circuits intégrés sur substrat de silicium, circuits universellement employés dans les systèmes électroniques, aussi bien « grand public » que de haute technologie.

I. ÉLABORATION DU SILICIUM MONOCRISTALLIN

I.1. Le silicium de qualité «métallurgique»

Le silicium élémentaire est produit dans un four électrique, à l'état liquide, par réduction carbothermique de la silice (sable de rivière ou de carrière), selon l'équation-bilan :

Il est ensuite solidifié en lingots ; sa pureté ne dépasse pas 95-98%.
Ql : Quelle est la variance du système où les quatre constituants de l'équation [1] sont à l'équilibre thermodynamique?

Le diagramme de la Figure 1, qui présente l'évolution avec la température de l'enthalpie libre de formation des différents composés pris en compte dans ce problème, permet de répondre graphiquement aux trois questions suivantes, sans effectuer le calcul du

de la réaction [1] :

Q2 : Quelle est la température d'inversion de la réaction [1] à la pression atmosphérique ?
Q3 : Pourquoi doit-on se placer au-dessus de cette température pour préparer le silicium élémentaire et non aut dessous?

Q4 : La réaction parasite de formation du carbure de silicium SiC (solide) selon :

est-elle possible à la température d' inversion ?
Les réponses aux questions 2 et 4 nécessitent d'effectuer sur le diagramme de la Figure 1 des constructions géométriques simples dont on précisera la nature.

QS : Comment se déplacerait la température d'inversion de la réaction [1] avec une diminution de pression ?

Figure 1: Evolution avec la température de l'enthalpie libre de formation, à partir des corps purs élémentaires, des divers composés mis en jeu. Chaque courbe correspond à la formation de 1 mole de composé.

I.2. La purification par distillation fractionnée

Le silicium «métallurgique ~~ est purifié par transformation en trichlorosilane SiHCb, distillation fractionnée de ce composé puis réduction par le dihydrogène.

Q6 : Dessiner la molécule de trichlorosilane en représentation perspective.
Q7 . Cette molécule est-elle optiquement active ? Pourquoi ?
Q8 : Ecrire et équilibrer l'équation-bilan renversable qui traduit, dans un sens, la formation du trichlorosilane à partir de silicium et de chlorure d'hydrogène gazeux et, dans l'autre, la réduction de ce composé par le dihydrogène. .

Q9 . Déterminer, en vous aidant de la Figure 1, les valeurs approchées des enthalpies standard de formation de

et de HCl .

QlO : En déduire, en le justifiant, le sens de déplacement de la réaction du Q8 ci-dessus (synthèse ou dissociation du trichlorosilane) quand on élève la température.

I.3. La fabrication des monocristaux

Le silicium issu de l'étape de réduction contient infiniment peu d'impuretés hormis celles qu'on a choisi de lui ajouter pour le doper « n » ou « p » (arsenic, bore, phosphore). Il n'est pas tenu compte de ces ajouts dans la suite. Un procédé de fusion-solidification très lente le transforme en lingots monocristallins. Ce silicium monocristallin est décrit par un système cubique à faces centrées dans lequel la moitié des sites tétraédriques contient un atome de silicium (structure type diamant). La Figure 2 présente une vue en perspective de la maille du silicium. Le paramètre de maille a (longueur de l'arête de la maille) est égal à

Figure 2 : Vue en perspective de la maille cubique du silicium. Les atomes noirs occupent les sommets de la maille, les atomes gris les centres des faces, les atomes blancs les lacunes tétraédriques, comme mentionné dans le texte.

Dans ce matériau monocristallin, on tronçonne puis on polit « miroir » des tranches fines (diamètre 15 cm , épaisseur

) dé deux types :
. Tranches [100] : surface des tranches contenant les atomes d'une des faces de la maille cristalline c.f c. du silicium, . Tranches [ 1111 ] : surface des tranches contenant les atomes de coordonnées (

) de la maille (a est le paramètre de la maille cubique).

Qll : En utilisant des cercles pour représenter les atomes de silicium, schématiser l'arrangement atomique à deux dimensions du plan atomique de la surface de chacune de ces tranches. Seuls les atomes dont les centres sont contenus dans le plan de surface seront représentés. On veillera à ce que ressorte expressément l'environnement d'un atome de silicium par ses plus proches voisins de ce plan.

Q12 : Calculer la densité atomique (atomes

) de chacun de ces plans.

II. GÉNÉRATION DES MOTIFS MICROMÉTRIQUES

Après une étape d'oxydation thermique générant une couche très fine de silice SiO 2 sur les tranches, les étapes de masquage et de gravure permettent d'obtenir des motifs de taille micrométrique, autorisant une très grande intégration des transistors élémentaires (VLSI : Very Large Scale Integration).

II.1. Le masquage

Il est réalisé par étalement d' un polymère photosensible qu' on détruit localement par insolation et développement chimique (résine positive). L'un des matériaux utilisés pour les insolations par Rayons

est le PMMA, polyméthacrylate de méthyle, obtenu par polymérisation de son monomère, le 2-méthyl, propénoate de méthyle.

Q13. Quelle est la formule développée de ce monomère?
Q14 : Dans le cas où la synthèse du PMMA est une réaction de polymérisation anionique induite par

, quelles sont les formules des deux anions monomères isomères qui peuvent se former ?

Q15 : L'un de ces deux anions isomères possède une stabilité remarquable due à un phénomène de résonance. Ecrire la relation de mésomérie en cause. On notera clairement les déplacements électroniques, les positions des doublets électroniques non liants et les charges électriques.

Q16 : Représenter le motif du matériau polymère PMMA.
Q17 : Par des considérations simples sur la force des bases mises en jeu, justifier le fait que l'anion amidure ne soit pas stable dans l'eau.

Q18 : Ecrire la réaction de cet anion avec l'eau.
II.2. La gravure chimique de la silice :

Gravure basique Dans les zones de la tranche non protégées par le PMMA, on peut dissoudre la couche de silice thermique sous forme de pentahydroxosilicate (IV) de potassium en utilisant une solution aqueuse d'hydroxyde de potassium.

Q19 . Ecrire l'équation bilan correspondante.
Q20 : Connaissant la solubilité moléculaire

de la silice et la constante de stabilité

, de l'anion pentahydroxosilicate (IV) à partir de la silice dissoute, déterminer aut-dessus de quel pH la dissolution devient quantitative (solubilité du silicium (IV) supérieure à

Gravure acide

Si on ne souhaite pas travailler en milieu basique, on emploie souvent des solutions d'acide fluorhydrique HF qui solubilisent la silice sous forme

Q21 : Quel est le nom de l'anion

?
Q22 : L'acide fluorhydrique est un acide faible de

voisin de 3,2. Quel est le pH d'une solution dans laquelle on a dissous

de HF ?

Q23 : Ecrire la réaction de solubilisation de la silice dans cette solution.
On observe sur le diagramme potentiel-pH du silicium en présence de fluor (-I) (Figure 4), qu'une telle solution est susceptible d'attaquer également le silicium élémentaire dès que la couche de silice aura disparu.

Figure 4 : Diagramme potentiel-pH du silicium à

en présence de solutions contenant 1 mol.

de fluor

; concentration de l'espèce dissoute SiF

mol.

Q24 : Ecrire cette réaction de dissolution du silicium.

L'observation expérimentale montre que, si l'attaque de la silice par HF est rapide à ce pH , celle du silicium est extrêmement lente.

Q25 : En déduire une valeur par défaut de la surtension du dihydrogène sur le silicium.

III. ENCAPSULATION DES CIRCUITS

Une fois terminés, les circuits intégrés sont encapsulés dans un matériau polymère qui autorise leur manipulation et leur confère une certaine protection contre les agressions extérieures (chocs, corrosion, ...). La molécule de la Figure 5 (DGEBA) permet, par exemple, de synthétiser certains de ces matériaux.

Figure 5 : Diglycidyléther du bisphénol A utilisable comme résine pour la préparation de polyépoxides d'encapsulation.

Q26 : Quelle est sa formule brute?