J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

CCINP Physique 1 PC 2013

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ccinp
🔗 Explorer
Banque
CCINP
Année
2013
Filière
PC
Matière
Physique
CCINP PCCCINP 2013PC PhysiquePhysique 2013
2025_09_04_08fcb3689a7ab14ae5dbg

EPREUVE SPECIFIQUE - FILIERE PC

PHYSIQUE 1

Durée : 4 heures

Abstract

N.B. : Le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

Les calculatrices sont interdites

L'épreuve comporte deux problèmes indépendants.
L'attention des candidats est attirée sur le fait que la notation prendra compte du soin, de la clarté et de la rigueur de la rédaction. Les candidats sont priés d'accorder une importance particulière aux applications numériques demandées, en veillant à l'unité et aux chiffres significatifs du résultat.

Formulaire

  • Pour tout nombre réel .
  • La décomposition en série de Fourier d'une fonction périodique de période est :
avec :

PROBLEME A : CONTRASTE INTERFERENTIEL

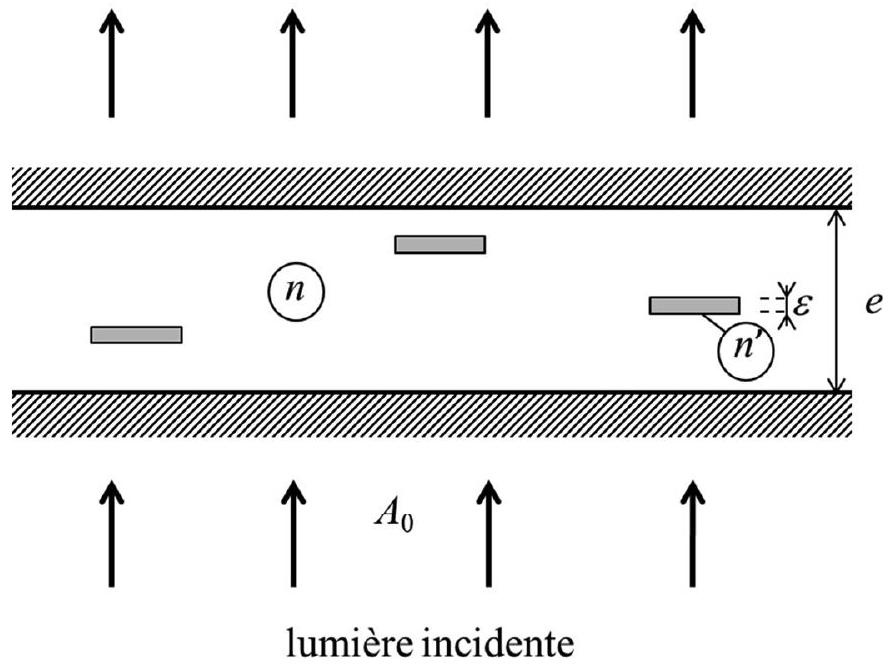
Sur la platine d'un microscope est posée une préparation très mince transparente, immergée dans un liquide d'indice et comprise entre deux lamelles de verre identiques dont les faces en regard, semi-argentées, sont parallèles. Les détails de la préparation peuvent être assimilés à de petites lames à faces parallèles d'indice d'épaisseur très faible, parallèles aux faces semi-argentées (figure 1). L'ensemble est éclairé par transmission en incidence normale par un faisceau parallèle de lumière monochromatique (raie verte d'une lampe spectrale à mercure : ) à l'aide d'un trou source disposé au foyer objet du condenseur non représenté dans la figure 1. Un objectif placé au-dessus de la préparation permet d'observer celle-ci.
Figure 1 : vue de profil de la préparation liquide sous microscope

A1- Observation en l'absence de détails

Les deux lamelles de verre semi-argentées peuvent être considérées comme deux miroirs semiréfléchissants de coefficients de réflexion et de transmission en amplitude et (nombres réels positifs inférieurs à 1) et introduisant un déphasage à leur traversée. Une onde se propageant dans la cavité ainsi formée émet à chaque aller-retour un rayon émergent. Les rayons émergents transmis sont parallèles entre eux et interfêrent à l'infini. En négligeant tout phénomène de réfraction (les rayons incidents sont considérés comme ayant une incidence normale aux lames) et tout phénomène d'absorption des miroirs et de la préparation liquide, l'amplitude complexe en un point à l'infini du rayon émergent s'écrit où est l'amplitude du rayon et sa phase.
A1.1- Exprimer le déphasage entre deux rayons émergents successifs en fonction de l'épaisseur de la cavité , de l'indice de réfraction du milieu et de la longueur d'onde de la lumière incidente dans le vide.
A1.2- Calculer le rapport des amplitudes de deux rayons successifs en fonction du coefficient de réflexion en amplitude des deux lames semi-réfléchissantes.
A1.3- En déduire l'amplitude complexe du rayon émergent, en prenant comme référence des phases, celle du rayon incident entrant à travers la lame inférieure dont l'amplitude complexe s'écrit .
A1.4- Calculer l'amplitude complexe en un point à l'infini résultant de la superposition de l'ensemble des rayons émergents de à l'infini, le coefficient de réflexion étant inférieur à 1 .
A1.5- Montrer que l'intensité recueillie à l'infini peut se mettre sous la forme: où sera exprimé en fonction de et en fonction de et .
A1.6- Pour , calculer .
A1.6.1- Déterminer les valeurs de qui correspondent à un maximum de . Que vaut , la valeur de ces maxima?
A1.6.2- Evaluer la valeur et la position des minima de .
A1.6.3- Calculer les valeurs de autour d'un maximum, tel que . En déduire la largeur à mi-hauteur du pic correspondant que l'on exprimera en fonction de . Simplifier en tenant compte de la valeur de .
A1.6.4- Tracer l'allure de .
A1.6.5- En déduire que l'intensité recueillie à l'infini ne peut être considérée comme non nulle que pour certaines valeurs de très réduites. En l'absence de détails, pour une préparation constituée uniquement d'un liquide homogène, quel serait l'aspect du champ observé ?

A2- Observation en présence de détails.

Les réflexions sur les faces d'un détail sont négligeables si bien qu'un rayon lumineux traversant un détail peut être considéré comme transmis intégralement en amplitude (pas d'absorption par le détail).
A2.1- Comme à la question A1.1, exprimer le déphasage entre deux rayons émergents successifs , mais dans une zone comportant un détail, en fonction des épaisseurs de la cavité et du détail , des indices de réfraction du milieu et du détail ' et de la longueur d'onde de la lumière incidente.
Montrer que peut s'exprimer comme avec dépendant uniquement de et . Calculer pour une préparation d'indice 1,515 contenant un détail d'épaisseur et d'indice de réfraction 1,520 . Remarquer que la valeur de est petite par rapport à celle donnant .
A2.2- Que devient l'intensité transmise dans une zone comportant un détail ?
A2.3- Calculer le contraste de l'image du détail par rapport au "fond", le contraste étant défini par .
Montrer que le contraste est de la forme où la constante dépend de et de .
A2.4- L'épaisseur de la préparation est choisie de manière à ce que (avec nombre entier). Pour les mêmes valeurs de et de trouvée à la question A1.6 et sachant que l'œil humain décèle un contraste minimal de 0,1 , le détail est-il visible ?
A2.5- Pour quelle valeur de , donc de l'épaisseur de la préparation, le contraste est-il maximal ? Quelle est alors l'épaisseur minimale d'un détail décelable (donner un ordre de grandeur) ? Proposer une méthode expérimentale pour rendre un détail suffisamment contrasté pour être observé.

PROBLEME B : UNE BALANCOIRE

Un enfant faisant de la balançoire (figure 2) est modélisé par une masse ponctuelle située en et suspendue en par une tige rigide, de masse négligeable et de longueur . Le champ de pesanteur , de norme , est supposé uniforme. L'angle que fait la tige de suspension avec la verticale est noté (figure 3). Les vecteurs unitaires et , tels que définis sur la figure 3, définissent un trièdre orthonormé direct lié à la balançoire.
Figure 2 : enfant assis sur sa balançoire
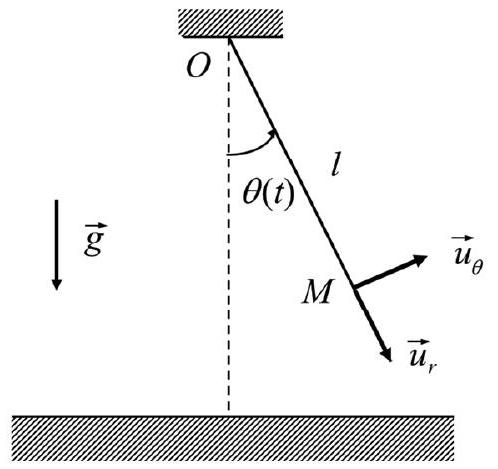
Figure 3 : schématisation de la balançoire et repère mobile associé
B1- A quelle condition, sur la durée de l'expérience, le référentiel terrestre peut-il être considéré comme galiléen ? On donnera un ordre de grandeur.
Cette condition sera supposée être vérifiée dans toute la suite du problème.
B2- Dans cette question, tout frottement de la tige sur son axe de rotation et tout frottement dû à la résistance de l'air sont négligés.
B2.1- Etablir l'équation différentielle du mouvement vérifiée par en utilisant trois méthodes :
B2.1.1- en appliquant le principe fondamental de la dynamique ;
B2.1.2- en appliquant le théorème de l'énergie cinétique ;
B2.1.3- en appliquant le théorème du moment cinétique.
B2.2- En déduire que le mouvement est plan.
Dans toute la suite du problème, les mouvements de la balançoire et de l'enfant seront étudiés dans le plan vertical de la figure 3.
B2.3- A quelle condition l'enfant assis sur la balançoire sera-t-il un oscillateur harmonique? Donner l'expression littérale de la pulsation propre correspondante.
Application numérique : l'enfant part d'un angle sans vitesse initiale. Avec les valeurs numériques suivantes: et , calculer la période de l'oscillateur harmonique, ainsi que la vitesse maximale de l'enfant.
B3- L'approximation de l'oscillateur harmonique est ici examinée en considérant les effets non linéaires. L'enfant part d'un angle positif sans vitesse initiale.
B3.1- En partant du théorème de l'énergie cinétique, étudié à la question (B2.1.2), donner l'expression de en fonction de et des paramètres caractéristiques du système. En déduire l'expression de la période sous forme d'une intégrale en fonction de et des paramètres caractéristiques du système. On précisera soigneusement les bornes d'intégration. On ne demande pas de calculer cette intégrale.
Retrouver le résultat de la question dans le cas des petites oscillations.
Une intégration numérique permet de dessiner la courbe représentative de la fonction cidessous (figure 4). Commenter cette courbe.
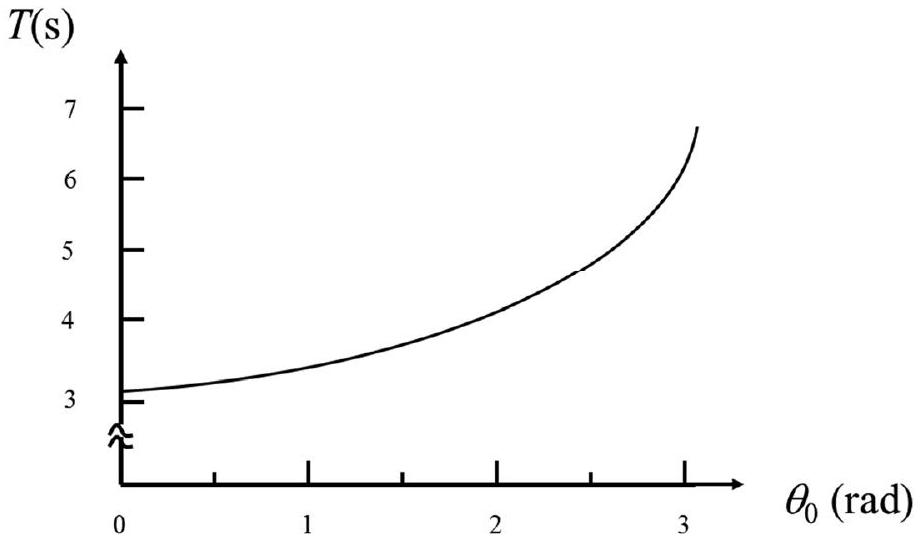
Figure 4 : période en fonction de l'angle de départ
B3.2- Posant , que devient l'équation différentielle du mouvement vérifiée par ?
B3.3- On cherche, pour l'équation différentielle approchée écrite en B3.2, une solution elle-même approchée de la forme :
ù
B3.3.1- En se limitant au premier ordre en , exprimer en fonction de et la pulsation fondamentale ainsi que le terme .
B3.3.2- Par rapport au mouvement harmonique, la courbe relative au mouvement réel a-t-elle une plus grande ou une plus petite période?
B3.3.3- Quelle est la pulsation du premier harmonique après le fondamental ?
B3.3.4- Dans le cas général où on ne se limiterait pas à des développements au premier ordre, quelle serait l'allure du spectre de la solution obtenu par analyse spectrale?
B4- Au point s'exercent des forces de frottement sur la tige. Le moment de ces forces (par rapport à ) est égal à où est une constante positive et .
B4.1- Quelle est la dimension de la constante ?
B4.2- Etablir l'équation différentielle à laquelle doit maintenant obéir .
B4.3- En supposant que l'angle reste suffisamment petit, à quelle inégalité doit satisfaire pour que le mouvement de l'enfant puisse être considéré comme un mouvement oscillatoire dont l'amplitude décroît avec le temps (mouvement pseudo-périodique) ?
Application numérique : considérant cette condition satisfaite, on approxime ici la pseudo-période à la période de la question B2.3. L'enfant part d'un angle sans vitesse initiale. On observe que l'amplitude du mouvement est réduite de moitié après 20 oscillations. Calculer la valeur de la constante avec les valeurs numériques données à la question .
B5- Les frottements (question B4) ont pour conséquence d'amortir le balancement de l'enfant et un deuxième enfant vient donc aider le premier enfant qui se balance à maintenir une amplitude constante en le poussant (figure 5) avec une force horizontale périodique non harmonique dont le module est représenté à la figure 6 .
Figure 5 : enfant sur sa balançoire poussé par un autre enfant
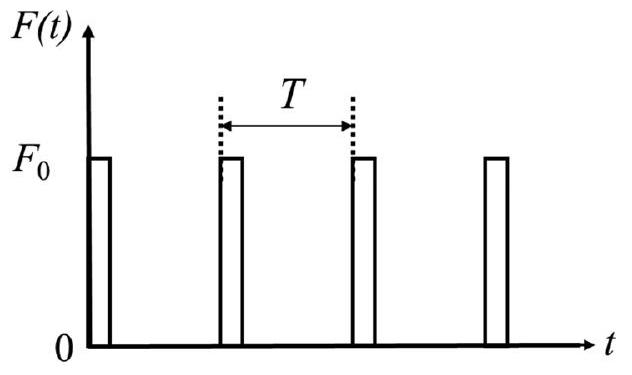
Figure 6 : profil de la force appliquée à l'enfant sur sa balançoire en fonction du temps
N.B. : il n'est pas nécessaire d'effectuer une analyse en série de Fourier de pour répondre aux questions B5.1, B5.2 et B5.3.
B5.1- A quel moment et à quelle fréquence l'enfant pousseur doit-il appliquer sa poussée sur l'enfant de la balançoire pour que son action soit la plus efficace possible ? Que vaut donc la période de la force pour que l'action de l'enfant pousseur soit la plus efficace possible ? (on supposera les frottements faibles dans cette question et dans les suivantes).
B5.2- Représenter sur un même graphe la fonction de la figure 6 et l'angle .
B5.3- Déterminer la puissance moyenne dissipée par les frottements en fonction de la pulsation du mouvement et l'amplitude du mouvement. En déduire le travail fourni par l'enfant pousseur après 20 oscillations de l'enfant se balançant (les valeurs numériques des différents paramètres sont toujours ceux donnés à la question B2).
B6- L'enfant se balançant décide de monter sur une autre balançoire, pour laquelle les frottements sont considérés comme totalement négligeables. Alors que l'enfant se balance, il décide de monter de plus en plus haut. Pour cela, il effectue les mouvements suivants au cours des phases oscillatoires successives, :
  • lorsque la balançoire passe par la position verticale, l'enfant accroupi se relève (de à );
  • de à , l'enfant reste debout;
  • lorsque la balançoire atteint , son amplitude d'oscillation maximale, l'enfant s'accroupit (de à );
  • de à , l'enfant reste accroupi ;
  • lorsque la balançoire repasse par la position verticale, l'enfant accroupi se relève (de à );
  • de à , l'enfant reste debout ;
  • lorsque la balançoire atteint , sa nouvelle amplitude d'oscillation maximale, l'enfant s'accroupit à nouveau (de à ) ;
  • de à , l'enfant reste accroupi.
Sur la figure 7 sont tracées la trajectoire et quelques positions du centre de gravité de l'enfant dans le référentiel galiléen lié au sol. Les passages de la position accroupie à debout et réciproquement sont considérés comme instantanés.
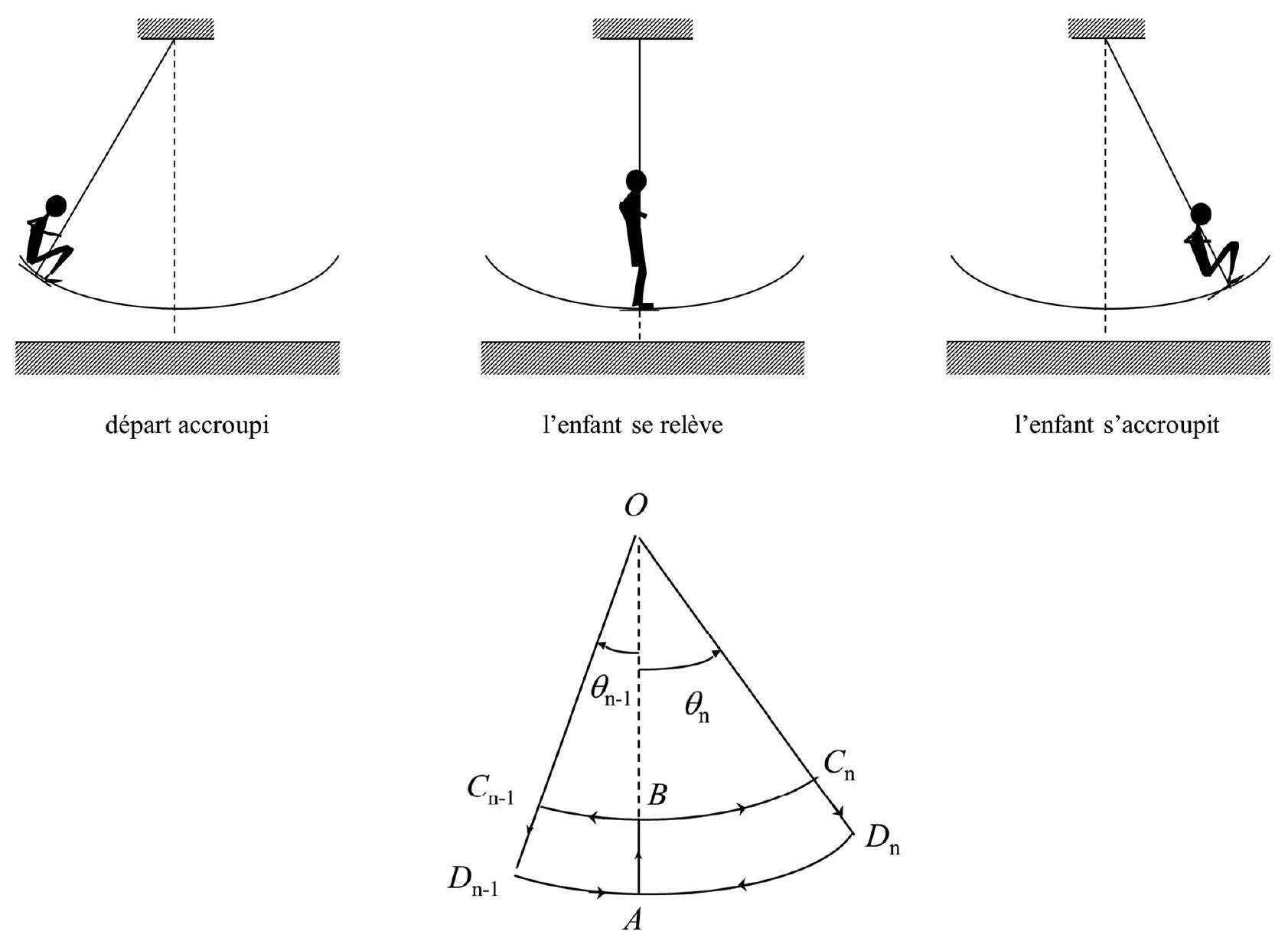
Figure 7 : mouvements de l'enfant sur sa balançoire
B6.1- Description qualitative.
B6.1.1- Dans un repère lié à la balançoire (c'est-à-dire un repère lié à la tige de suspension et au siège de la balançoire), identifier les forces extérieures au système.
B6.1.2- Evaluer alors dans ce même repère lié à la balançoire, pour chacune des forces extérieures au système, le signe du travail qu'elles produisent sur un demi-cycle .
B6.1.3- En appliquant alors le théorème de l'énergie cinétique sur le demi-cycle , en déduire que le travail des forces intérieures dû au mouvement du corps de l'enfant, qui se relève et s'accroupit, est de signe positif.
B6.1.4- Il est rappelé que pour tout système de points matériels, le travail des forces intérieures se conserve dans un changement de référentiel (il n'est pas demandé de démontrer cette propriété). En appliquant le théorème de l'énergie cinétique dans le référentiel galiléen lié au sol, en déduire que le mouvement du corps de l'enfant, qui se relève et s'accroupit, permet à la balançoire de monter de plus en plus haut.
B6.2- Modélisation simplifiée de la balançoire et de l'enfant.
On schématise la balançoire et l'enfant comme un pendule de masse fictive (constante) accrochée à un fil de longueur variable dépendant de la position angulaire de repérage : .
B6.2.1- Calculer le moment cinétique, , du pendule au point dans le référentiel galiléen lié au sol.
B6.2.2- En appliquant le théorème du moment cinétique dans le référentiel galiléen lié au sol, donner l'équation vérifiée par .
B6.2.3- En notant les élongations successives maximales (figure 7), montrer la relation :
(on pourra multiplier chacun des membres de l'équation donnée à la question B6.2.2 par la quantité ).
B6.2.4- Montrer que les positions angulaires extrémales successives, et , obéissent à une loi de récurrence faisant intervenir et .
On prendra pour et pour .
B6.2.5- En déduire les valeurs des positions angulaires extrémales atteintes par l'enfant sur sa balançoire.
B6.2.6- Si l'enfant démarre sans vitesse initiale, quelle est la position la plus avantageuse pour démarrer? La balançoire pourrait-elle faire accomplir un tour complet autour de son axe de rotation («grand soleil» comme à la barre fixe) ?
B7- Une autre manière de faire monter sa balançoire est la suivante : l'enfant peut rester assis et mettre son dos alternativement en avant ou en arrière tout en repliant puis étendant ses jambes afin de faire lever ou abaisser son centre de gravité.
En supposant comme précédemment que la masse de la balançoire est négligeable, on modélise la balançoire et l'enfant comme un ensemble de deux masses articulées. La masse totale de l'enfant est en notant la masse du corps en (la longueur de la balançoire est ) et la masse des jambes (la distance entre le centre de masse des jambes - qui est situé environ à la position des genoux - et le point est comme indiqué sur la figure 8).
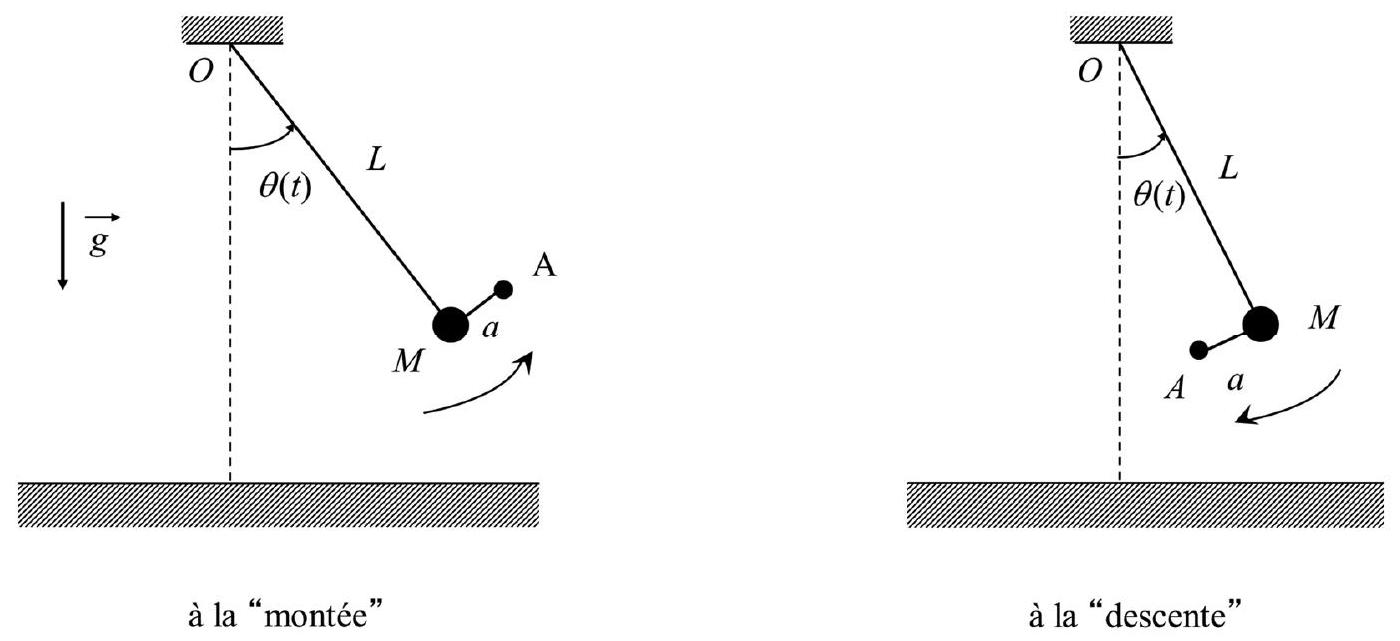
A la montée, l'enfant met et maintient ses jambes en "avant" tandis qu'à la descente l'enfant met et maintient ses jambes "en arrière". Pour simplifier, il est supposé que la direction fait un angle droit avec la direction à la "montée" comme à la "descente", tel qu'indiqué à la figure 8 .
Figure 8 : positions de l'enfant et de ses jambes assis sur sa balançoire
B7.1- Equation du mouvement.
B7.1.1- Calculer le moment cinétique de l'enfant, , au point dans le référentiel galiléen lié au sol.
B7.1.2- Calculer le moment des forces de pesanteur par rapport à l'axe , dans le cas où la balançoire est dans une phase de montée et dans le cas où la balançoire est dans une phase de descente. On pourra introduire l'angle tel que .
B7.1.3- En appliquant le théorème du moment cinétique, montrer que les équations du mouvement sont de la forme :
à la montée :
à la descente :
avec . On explicitera les termes et en fonction de , et .
B7.2- Etude des petites oscillations.
B7.2.1- Dans le cas de petites oscillations, donner les équations linéarisées du mouvement à la montée et à la descente.
B7.2.2- Montrer que le mouvement est l'analogue d'un oscillateur harmonique excité, d'équation dont on donnera sa pulsation propre et dont on représentera graphiquement la fonction excitatrice en fonction du temps (à l'instant initial l'enfant part avec les jambes tendues, en "avant" avec ).
B7.2.3- Décomposer la fonction excitatrice en série de Fourier et montrer que son expression est :
B7.2.4- Montrer que dans cette série, il y a un terme susceptible de conduire à une résonance. Dans ce cas et en l'absence d'amortissement, que devient l'amplitude des oscillations?
B7.2.5- Donner la solution de l'équation différentielle trouvée à la question B7.2.2 pour les termes non résonants.
B7.2.6- Donner la solution de l'équation différentielle trouvée à la question B7.2.2 pour le terme résonant. La solution sera recherchée sous la forme : où et sont deux constantes. Quel est le sens physique de cette solution pour ce terme résonant?
B7.2.7- En déduire l'expression générale de la solution .
B7.2.8- L'enfant se lance sans vitesse initiale, les genoux (c'est-à-dire le centre de masse de ses jambes) à la verticale du point de suspension (figure 9). En déduire les constantes d'intégration de l'expression de la variation angulaire déterminée à la question précédente.
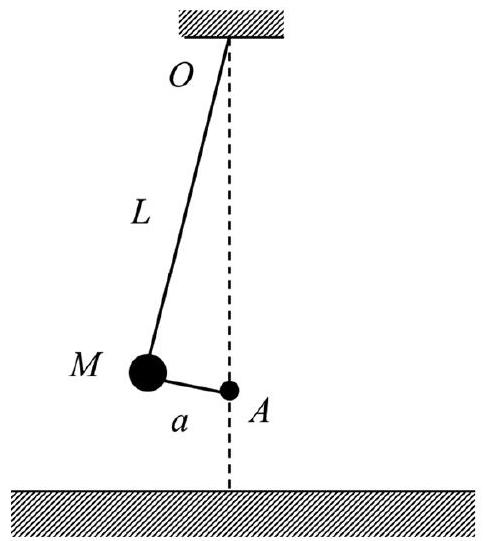
Figure 9 : schématisation de la position initiale de départ de l'enfant sur sa balançoire
On pourra utiliser le résultat mathématique suivant : .
Application numérique : pour une balançoire de longueur , un enfant de masse , ayant une longueur de jambe et une masse de jambes , la figure 10 présente le profil de la variation angulaire dans deux situations différentes. Commenter ces courbes, en expliquant quels mouvements l'enfant opère. Reproduire qualitativement ces courbes en représentant sur le même graphe la fonction .
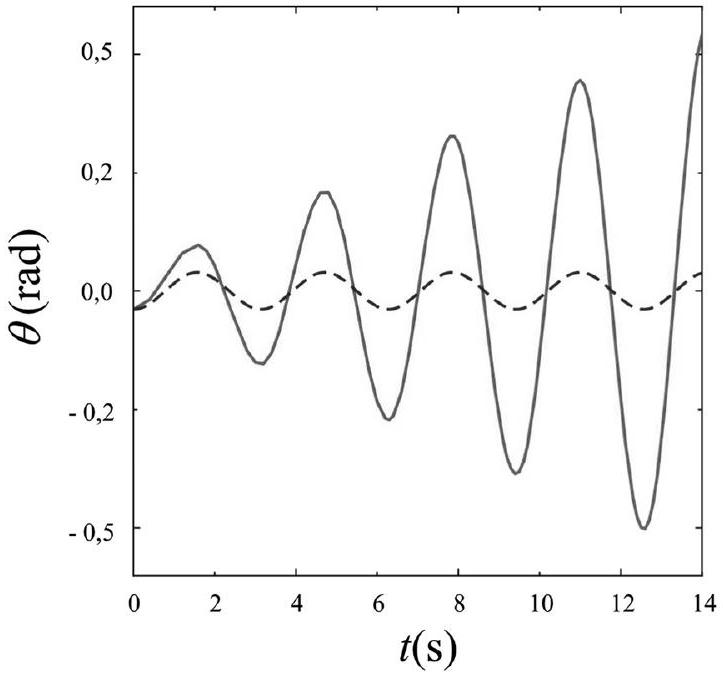
Figure 10 : profil de variation angulaire en fonction du temps dans deux situations différentes

Fin de l'énoncé

CCINP Physique 1 PC 2013 - Version Web LaTeX | WikiPrépa | WikiPrépa