Version interactive avec LaTeX compilé

CCINP Physique 1 PC 2005

Notez ce sujet en cliquant sur l'étoile

0.0(0 votes)

🔗 Explorer

CCINP PC CCINP 2005 PC Physique Physique 2005

2025_09_04_df1f2c0a3030f3ee944eg

Les calculatrices sont autorisées. Les deux problèmes sont indépendants. On fera l'application numérique chaque fois que cela est possible. Le symbole SI désigne l'unité homogène à la grandeur physique considérée, dans le cadre du Système International d'unités.

N.B.: Le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

Problème I L'ASCENSEUR SPATIAL

L'ascenseur spatial appartient au domaine de la science-fiction. Le concept, imaginé en 1960 par l'ingénieur soviétique Youri N. Artsutanov, fut popularisé par le romancier anglais Arthur C. Clarke en 1979 ("The fountain of paradise"). L'idée consiste à envoyer un câble très résistant au dessus de l'équateur et à s'en servir pour lever des charges en direction de l'orbite terrestre, tel un ascenseur géant. Le but de ce problème est d'étudier quelques aspects physiques d'une telle réalisation.
Données: Masse de la Terre

, rayon équatorial de la Terre

, constante de gravitation

, accélération de la pesanteur moyenne à la surface de la Terre (équateur)

, vitesse angulaire de rotation de la Terre par rapport aux étoiles lointaines

rad.s

I. 1 Mouvements orbitaux

La Terre est assimilée à un corps de symétrie sphérique. On néglige ici la masse et l'influence de la Lune, considérée comme un satellite léger. Les distances radiales

sont mesurées par rapport au centre de la Terre.

I.1.1 Trouver la valeur du champ de gravité régnant à la surface de la Terre en fonction de et . On pourra appliquer, par exemple, le théorème de Gauss pour à la surface de la Terre. Y a-t-il une différence entre et ?
I.1.2 Rappeler la relation entre le rayon de l'orbite circulaire d'un satellite et sa période de révolution. Exprimer ce rayon en fonction de .
I.1.3 Calculer, en jours, la période de révolution de la Lune, en assimilant son orbite à un cercle de rayon 384000 km .
I.1.4 Pour quelle distance un satellite est-il immobile dans le référentiel de la Terre ? Comment s'appelle cette orbite ?

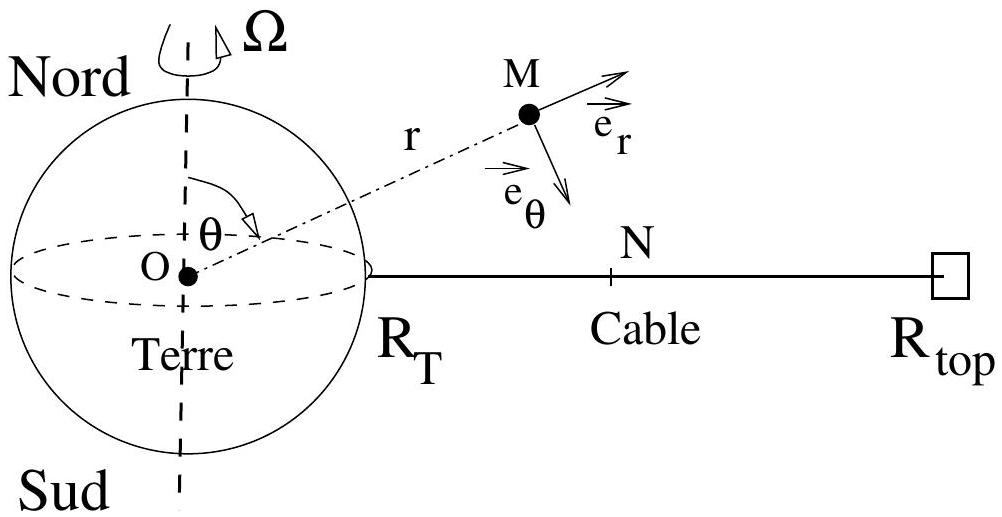
Figure 1

I. 2 Equilibre du câble

Le câble de l'ascenseur (Figure 1) possède une masse par unité de longueur

qui peut éventuellement dépendre de l'altitude (dans le cas où la section du câble varie, ou si le câble est élastique). Le câble est positionné exactement à la verticale de l'équateur. On supposera qu'un équilibre stable du câble est possible, résultant d'un équilibre entre la force de gravité, la force d'inertie de rotation dans le référentiel Terrestre

, et la force tensile

du câble.

I.2.1 Rappeler la différence entre le référentiel géocentrique et le référentiel Terrestre . Lequel des deux est le plus proche d'un référentiel Galiléen?
I.2.2 Donner dans un repère de coordonnées sphériques (Figure 1), lié au référentiel , l'expression de la force d'inertie d'entraînement et de la force de gravité terrestre en fonction de la distance d'un objet de masse .
I.2.3 En tout point d'altitude , la partie supérieure du câble exerce sur la partie inférieure une force , où est une fonction de signe positif, dont l'effet est de s'opposer à un allongement du câble. Montrer que l'équilibre du câble implique l'équation suivante:

I.2.4 Le câble se termine à une altitude supérieure à par une masse . En supposant la masse linéique du câble constante, calculer la valeur de la tension en fonction de et , pour toute valeur supérieure à .
I.2.5 Montrer que si la masse est trop faible, ou l'altitude insuffisante, la tension prendra une valeur négative. Cette valeur négative, synonyme de travail en compression, se traduirait vraisemblablement par un effondrement du câble. En déduire donc un critère de stabilité du câble de l'ascenseur. On s'appuiera sur l'étude des variations de la fonction .
I.2.6 Un câble de hauteur est-il stable en l'absence de masse ?

I. 3 Masse et résistance du câble

Le câble possède un rayon

et une section

. On appelle contrainte

, la valeur de la force

par unité de section (

) du câble. La résistance d'un matériau homogène dépend de la valeur de

qui ne doit pas dépasser une valeur critique

propre à chaque matériau. L'application d'une contrainte supérieure à

entraîne une déformation non-élastique, irréversible du matériau, puis éventuellement ensuite sa rupture.

I.3.1 En quelle unité bien connue s'exprime ?
I.3.2 Le matériau a une masse volumique . Exprimer la masse linéique en fonction de et puis de et .
I.3.3 On considère un câble, de section constante, dont la tension est toujours positive. Montrer que la tension du câble passe par un maximum. En déduire que l'équilibre du câble implique que le matériau doit résister à une contrainte au moins égale à que l'on exprimera en fonction des données du problème. Comment le rayon du câble influe-t-il sur la solidité de l'édifice?
I.3.4 Les valeurs numériques de et sont respectivement:

La résistance de l'acier et du kevlar vous semble-t-elle suffisante pour assurer la stabilité de l'édifice? Le module de Young de l'acier est de 200 GPa et celui du kevlar de 35 GPa (

). Calculer dans chaque cas l'allongement relatif

qu'impliquerait un câble utilisant ces matériaux au voisinage de

I.3.5 Les espoirs actuels sont fondés sur les nanotubes de carbone, supposés résister à SI, pour une masse volumique d'environ . Un câble spatial en nanotubes de carbone serait-il assez solide?
I.3.6 Pour fabriquer un câble de masse optimale, il suffit de faire varier la section du câble avec la hauteur de façon à ce que la résistance du câble soit juste suffisante pour supporter une tension . En faisant intervenir la contrainte critique et la masse volumique du matériau, montrer que la masse linéique devient proportionnelle à la tension .
I.3.7 Ecrire et résoudre l'équation différentielle de I.2.3 dans cette situation.
I.3.8 Tracer l'allure de la fonction obtenue en fonction de peut-elle devenir négative ? On estime que pour lever une charge de 10 tonnes, la tension du câble doit être au moins égale à , de sorte que la surcharge dûe à la masse supplémentaire ne dépasse pas de au sol. Calculer le rapport entre la tension maximale du câble et la tension du câble au niveau du sol dans le cas de l'acier et d'un câble en "nanotubes".

Nota Bene : les plus longues fibres de nanotube de carbone actuelles ne mesurent pas plus de

de long, et l'épissage d'un câble de nanotubes nécessite encore une révolution technologique.

I. 4 Stabilité du dispositif

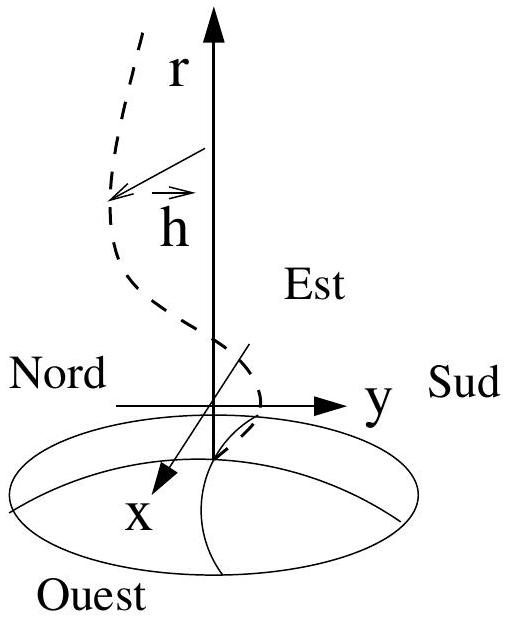
Figure 2

I.4.1 Pour étudier la propagation des vibrations le long du câble, nous assimilons celui-ci à une corde homogène de masse linéique constante et de tension constante . La gravitation ne perturbe pas les oscillations transverses du câble. La déviation du câble par rapport à la verticale (Figure 2) obéit à l'équation :

A quelle vitesse les ondes se propagent-elles le long du câble ?

I.4.2 La base et l'extrémité du câble, à la hauteur sont supposées fixes (si nécessaire au moyen d'un dispositif stabilisateur en haut du câble). Pour simplifier, on suppose que et sont constantes et que le rapport vaut .
Trouver la fréquence fondamentale de vibration du câble. Quelles sont les autres fréquences de vibration possibles ?
I.4.3 Comparer ces fréquences au phénomène périodique des marées lunaires (de période environ 12 heures). Quel phénomène physique est susceptible de se produire si les périodes de vibration propres du câble sont trop proches de 12 h ?
I.4.4 Effet du vent : un vent de vitesse souffle régulièrement sur le câble entre le sol et d'altitude. Si le câble mesure de diamètre, sachant que la masse volumique de l'air est , et sa viscosité de Pa.s, calculer le nombre de Reynolds de l'écoulement autour du câble. On montre qu'à de l'ordre de, ou inférieur à l'unité, la force de friction de l'air sur le câble est de :

alors qu'à nombre de Reynolds élevé, la force de friction de l'air est environ :

Choisir l'expression adéquate et calculer la force exercée par le vent sur le câble, l'inclinaison qui en résulte et le déplacement induit à l'altitude

. Prendre

au voisinage du sol, et un câble de masse volumique

I.4.5 Séisme : lors d'un séisme, un train d'ondes d'amplitude 1 m est engendré à la base du câble pendant 10 s . Sur quelle longueur s'étend le train d'ondes? Considérer la même valeur de , de diamètre et masse volumique du câble qu'à la question précédente.
I.4.6 L'énergie mécanique (cinétique et potentielle) du câble vaut, par unité de longueur,

L'ébranlement est sinusoïdal de fréquence 1 Hz . Quelle est l'énergie moyenne totale du train d'onde?

I. 5 Freinage électromagnétique

Nous venons de voir que l'un des problèmes est de dissiper l'énergie associée aux vibrations du câble (marées, séismes, tempêtes...). L'idée est de mettre à profit l'existence du champ magnétique permanent de la Terre pour créer dans le câble des courants induits "de Foucault". Le câble est donc parcouru de fils de cuivre de conductivité

, ou, de façon équivalente, de résistivité

. La section totale du fil de cuivre est supposée égale à

, et on néglige l'influence du cuivre sur la masse linéique du câble, de diamètre

et de densité

I.5.1 La dynamo Terrestre engendre un champ magnétique ressemblant à un dipôle magnétique orienté suivant l'axe de rotation de la Terre. Dessiner l'allure des lignes de champ magnétique autour de la Terre.
I.5.2 Dans un repère de coordonnées sphériques dont l'axe coïncide avec l'axe de rotation de la Terre, la valeur du champ magnétique est :

Sachant que l'intensité du champ magnétique Terrestre est de l'ordre de

à Paris (

de latitude Nord), calculer la valeur de

. Donner la valeur en tesla de

à l'altitude

, dans le plan équatorial.

I.5.3 On appelle l'axe Nord-Sud et l'axe Est-Ouest du plan tangent à la surface du sol, au voisinage de la base du câble (cf Figure 2). La déviation à la verticale s'écrit . Le champ magnétique est localement uniforme et dirigé suivant . Donner l'expression du champ électromoteur induit par un déplacement du câble .
I.5.4 Calculer l'intensité induite dans le câble conducteur de section par ce déplacement, en supposant que le champ électromoteur est seul présent.
I.5.5 En considérant la force de Laplace, justifier que l'équation pour devienne:

avec

que l'on déterminera. Que devient l'équation pour

I.5.6 Calculer la puissance de la force de Laplace pour un segment de câble compris entre et . Que devient cette puissance ? Comparer la puissance dissipée à l'énergie mécanique donnée ci-dessus, dans le cas d'un ébranlement sinusoïdal (question I.4.6). Sur quelle échelle de temps caractéristique ce mode d'amortissement agit-il ? Les vibrations suivant sont-elles amorties?
I.5.7 En fait, la dynamo Terrestre n'est pas exactement alignée suivant l'axe de rotation de la Terre. Il en résulte que le champ magnétique possède une petite composante verticale suivant . Justifier que les équations pour et deviennent couplées.

Notes finales : Les problèmes techniques liés à une telle réalisation sont multiples. Citons entre autres la résistance aux débris spatiaux, la corrosion due aux radicaux libres de la haute atmosphère, la mise en place du câble...L'hypothèse d'une décharge de la haute atmosphère par un câble conducteur a été évoquée, et doit être évitée.

Problème II Optique physique et photographie

Données : célérité de la lumière dans le vide

, constante de Planck

, permittivité diélectrique du vide

, perméabilité magnétique

. L'espace est rapporté à un repère orthonormé

II. 1 L'énergie lumineuse

Une onde plane monochromatique de longueur d'onde

se propage dans le vide. Le champ électrique en un point (

) et à l'instant

est, en notation complexe :

où

désigne le vecteur unitaire dirigé suivant l'axe

, et

l'unité des nombres imaginaires:

II.1.1 Calculer la pulsation et la norme du vecteur d'onde .
II.1.2 Donner l'expression du champ magnétique associé.
II.1.3 Donner l'expression du vecteur de Poynting. Calculer sa valeur moyenne temporelle en un point donné.
II.1.4 La puissance moyenne transportée par l'onde, par unité de surface, est de . A quelle amplitude du champ électrique ce flux énergétique correspond-il ?
II.1.5 A combien de photons par seconde et par mètre carré cette intensité correspond-elle?

II. 2 Courbe de noircissement d'une émulsion photosensible

On considère une réaction photochimique (totale)

, de constante cinétique

, où

désigne le réactif,

le produit et

un photon. On suppose que l'on peut traiter les photons comme une espèce chimique de concentration

. La réaction est élémentaire, et sa cinétique est du second ordre. Le milieu est soumis à une irradiation constante de la part d'un faisceau lumineux, de sorte que la "concentration"

peut être considérée comme constante et proportionnelle à la valeur moyenne du carré du champ électrique

II.2.1 Ecrire une équation cinétique pour les concentrations et des espèces et .
II.2.2 A l'instant , la concentration de A est , uniforme, et . On appelle le temps d"exposition, c'est-à-dire le temps durant lequel la réaction photochimique a lieu. Exprimer les concentrations et des espèces A et B en fonction de , et .
II.2.3 La réaction provoque le noircissement d'un film photographique. On appelle "opacité" du film, après développement, le rapport entre l'intensité lumineuse transmise à travers le film et l'intensité lumineuse incidente. Le développement du film ne révèle une exposition que si la concentration est supérieure à une valeur de seuil , et on fait l'hypothèse que l'opacité est proportionnelle à la différence . Un film non exposé présente toujours un léger voile d'opacité égale à . Montrer que ce modèle rend compte qualitativement de la courbe de noircissement d'un film photographique schématisée sur la Figure 3.

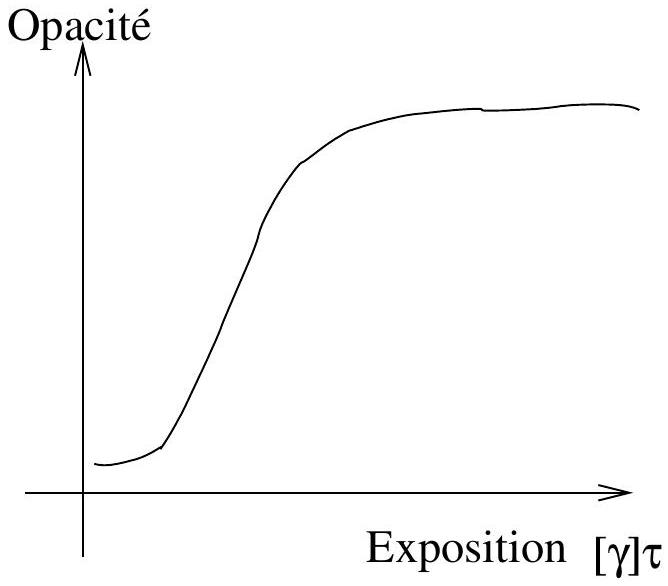
Figure 3

II. 3 Montage

Un laser de longueur d'onde

est utilisé dans le montage de la Figure 4 ci-dessous. Un dispositif optique forme une onde plane monochromatique, puis une lame semi-réfléchissante (en A) sépare le faisceau en deux. Après une réflexion en

, le faisceau numéro 2 vient interférer en

avec le faisceau numéro 1 . On néglige le déphasage dû à la lame semi-réfléchissante sur le trajet du faisceau numero 1, et on admet que les réflexions en A et B ne changent pas la phase du faisceau numero 2. On introduit les distances

. Tous les effets dûs à la polarisation de la lumière sont négligés et le champ électrique est traité comme un champ scalaire.

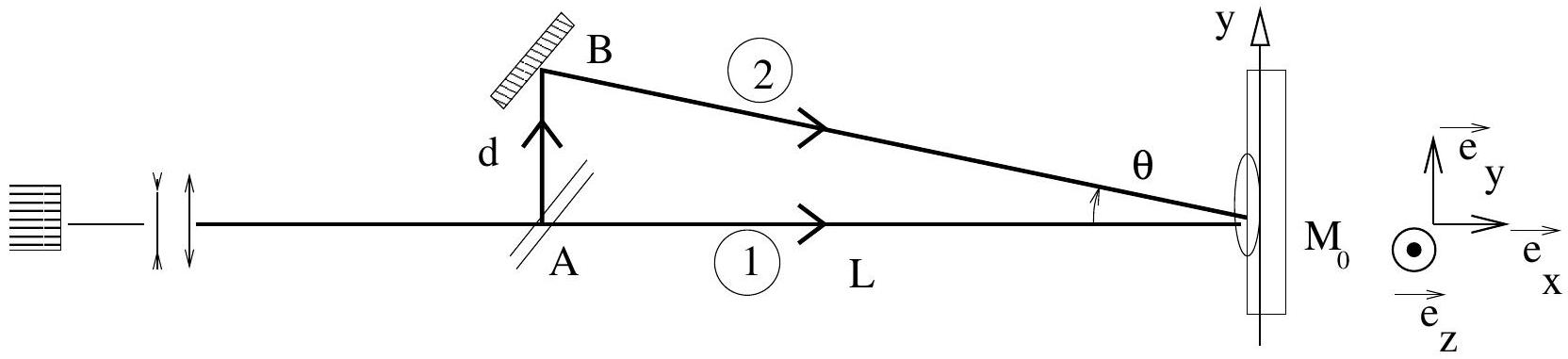
Figure 4

II.3.1 Qu'observe-t-on sur l'écran? Illustrer par un schéma.
II.3.2 Pourquoi utilise-t-on une seule source de lumière et une lame semi-réfléchissante plutôt que deux sources de lumière pour les rayons 1 et 2 ?
II.3.3 Soit le point de coordonnées et . Calculer la différence de marche entre le rayon 1 ( AM ) et le rayon 2 ( AB et BM ). En supposant que les faisceaux 1 et 2 sont des ondes planes monochromatiques dont les directions font entre elles un angle (Figure 5), calculer la différence de phase entre les deux ondes pour un point de coordonnées voisin de M. Démontrer que :

où

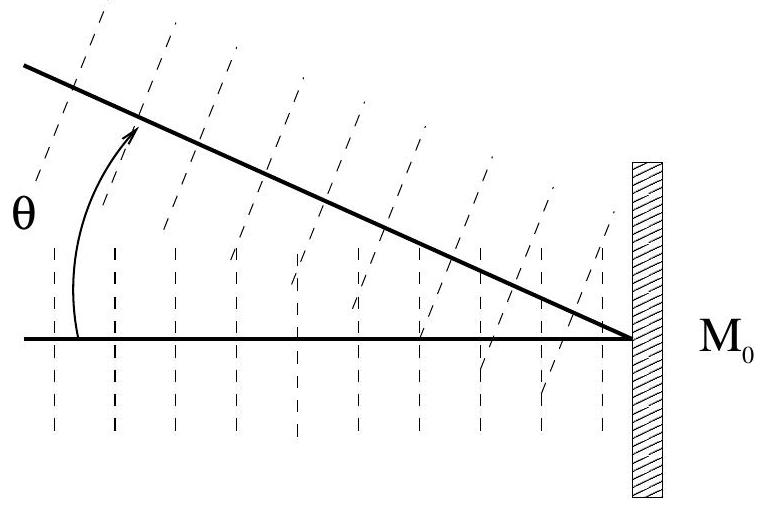
est une longueur que l'on exprimera à l' aide de

Figure 5

II.3.4 Le champ électrique en vaut

Calculer l'intensité lumineuse moyenne, proportionnelle à

, en un point

proche de

. On notera

II.3.5 On place sur l'écran un film photographique. Après développement, le film présente une succession de bandes transparentes et opaques. Combien de bandes transparentes par millimètre apparaissent sur le film ? Application : .

II. 4 Dispersion de la lumière

Le film photographique de la question II.3.5, après développement, est éclairé par l'arrière (à gauche sur la Figure 6) par un faisceau monochromatique cohérent de longueur d'onde

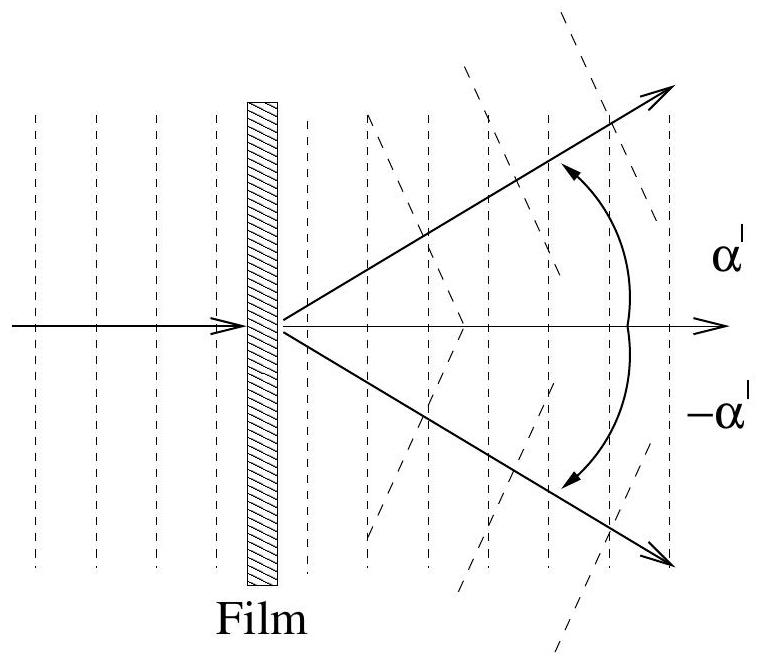
. On s'intéresse à l'onde transmise (à droite sur la figure), et on applique le théorème de Huyghens-Fresnel à la surface du film. Chaque point du film se présente comme une source secondaire cohérente d'amplitude :

Figure 6

II.4.1 Justifier que l'onde transmise est équivalente à une superposition de trois ondes planes, l'une se propageant horizontalement, les deux autres respectivement suivant un angle et avec l'horizontale. Indication : on pourra, soit faire un calcul, soit considérer l'amplitude du champ électrique que produiraient ces trois ondes dans le plan ( ) en l'absence du film.
II.4.2 On remplace le faisceau de longueur d'onde par un faisceau de longueur d'onde différente. Montrer que l'angle est modifié en . Ecrire une relation entre et . En déduire que ce film photographique possède le pouvoir de disperser la lumière blanche ou polychromatique. Comment s'appelle un tel dispositif optique?