Version interactive avec LaTeX compilé

CCINP Option Informatique MP 2022

Notez ce sujet en cliquant sur l'étoile

0.0(0 votes)

🔗 Explorer

CCINP MP CCINP 2022 MP Info Info 2022

2025_08_29_947eea36944e6caecb1bg

ÉPREUVE MUTUALISÉE AVEC E3A-POLYTECH ÉPREUVE SPÉCIFIQUE - FILIÈRE MP

INFORMATIQUE

Durée : 4 heures
N.B. : le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

RAPPEL DES CONSIGNES

Utiliser uniquement un stylo noir ou bleu foncé non effaçable pour la rédaction de votre composition ; d'autres couleurs, excepté le vert, peuvent être utilisées, mais exclusivement pour les schémas et la mise en évidence des résultats.
Ne pas utiliser de correcteur.
Écrire le mot FIN à la fin de votre composition.

Les calculatrices sont interdites.

Le sujet est composé de trois parties, toutes indépendantes.

Partie I - Automates

L'objectif de cette partie est de proposer quelques éléments autour d'un automate, dit augmenté, construit autour d'un automate fini non déterministe et d'un sous-ensemble d'états.

Définition 1 (Automate fini non déterministe)
Un automate fini non déterministe est un quintuplet

avec :

un ensemble fini non vide d'états, de cardinal ;
un alphabet;
l'ensemble des états initiaux;
une fonction de transition : si et désigne l'ensemble des états de tels qu'il existe une transition étiquetée par de vers ;
l'ensemble des états finaux.

Définition 2 (Automate augmenté)
Soient

un automate fini non déterministe et

un sous-ensemble d'états de

. On appelle automate augmenté par

la paire (

), que l'on notera par la suite

La notion de calcul est la même entre

: un calcul dans

est une séquence d'états

telle qu'il existe toujours au moins une transition entre deux états successifs de cette séquence. Le mot construit par concaténation des étiquettes de chacune des transitions est alors reconnu par l'automate.
L'ensemble

introduit la notion de calcul réussi au seuil

.
Définition 3 (Calcul réussi au seuil

)
Soit

un automate augmenté. Un calcul passant par les états

est dit réussi au seuil

si :
i)

;
ii)

;
iii) pour tout

tel que

Définition 4 (Langage reconnu par un automate augmenté au seuil

)
Soit

un automate augmenté et

. Le langage reconnu par

au seuil

, noté

, est l'ensemble des calculs réussis par

au seuil

On considère, pour les questions 1 à 3 , l'automate de la figure 1 , où

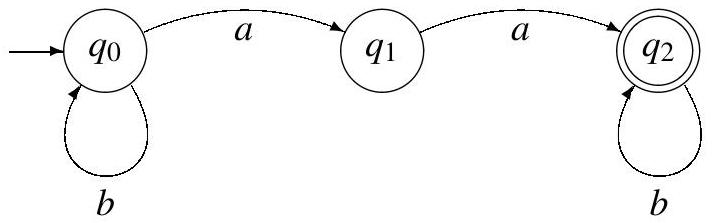
Figure 1 - Automate exemple

Q1. Donner sans justification

.
Q2. Donner, en justifiant votre réponse,

.
Q3. Soit

. Donner, en justifiant votre réponse, le cardinal de

en fonction de

, où

est l'ensemble vide.

Q4. Donner, sans justification, un majorant des calculs réussis au seuil

ne passant par aucun état de

Q5. Soit maintenant un calcul réussi au seuil

qui passe au moins par un état de

. On note

la suite des états correspondants et

la suite des indices dans

correspondant aux états de

. Donner, sans justification, en fonction de

:
i) une majoration de

;
ii) un encadrement de

;
iii) une majoration de

pour

Q6. Soit

un automate augmenté, avec

, où

est l'ensemble des états de l'automate. Pour

, construire, en justifiant votre construction, un automate fini à (

)

états reconnaissant

Partie II - Autour des tas

Cette partie comporte des questions de programmation qui seront abordées en utilisant exclusivement le langage Python (Informatique Pour Tous).
L'objectif est ici d'étudier et d'implémenter quelques outils autour d'une structure de données appelée tas binomial. Un tas binomial est une structure assez proche du tas binaire (utilisé par exemple pour réaliser une file de priorité), pour lequel la procédure de fusion de deux tas est efficace et peu complexe.

II. 1 - Arbre binomial

Définition 5 (Arbre enraciné)
Un arbre enraciné est un graphe acyclique orienté possédant une unique racine et tel que tous les nœuds sauf la racine ont un unique parent.

La figure 2 présente un exemple d'arbre enraciné dans lequel

est la racine.

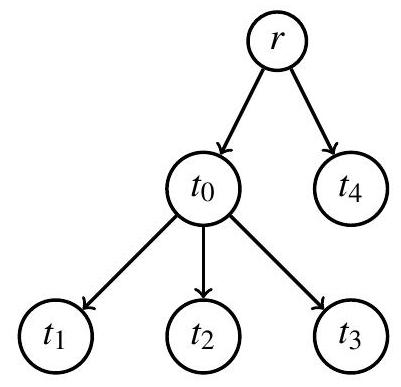
Figure 2 - Exemple d'arbre enraciné

On définit un arbre enraciné (non vide) par un couple (

), où r est la valeur de la racine et

est la liste de ses fils, chaque

étant un arbre. Un arbre vide est défini par None. Par abus de notation, on confond dans la suite la racine de l'arbre et sa valeur, ainsi que les fils d'un arbre avec leur racine.
Q7. Écrire les fonctions Python:

Vide(a) qui renvoit True si l'arbre a est vide, False sinon;
Racine(a) qui renvoit la racine de a si a est non vide;
Fils(a) qui renvoit la liste des arbres, fils de la racine de a.

Définition 6 (Arbre binomial)
Un arbre binomial

d'ordre

est un arbre enraciné dans lequel les fils de chaque nœud sont ordonnés. Il est défini récursivement comme suit :
i)

est constitué d'un nœud unique, la racine;
ii) pour

, soit

un arbre non vide.

est un arbre binomial d'ordre

si :

est un arbre binomial d'ordre ( );
( ) est un arbre binomial d'ordre ( );
la racine de a une valeur supérieure ou égale à r .

La figure 3 donne un exemple d'arbre binomial d'ordre 3. Les valeurs dans l'arbre sont des entiers.

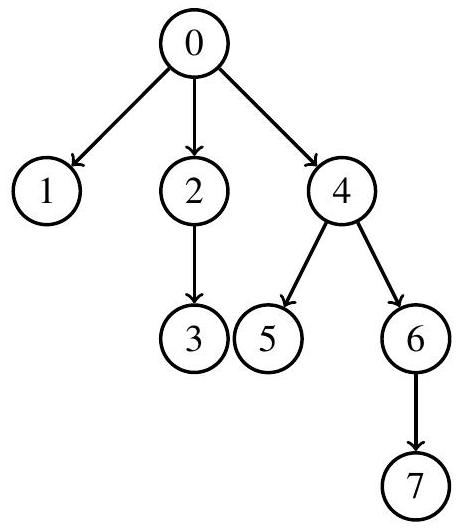
Figure 3 - Exemple d'arbre binomial d'ordre 3

Q8. Écrire une fonction Python ArbreBinomial(a1,a2) qui construit, à partir de deux arbres binomiaux a1 et a2 d'ordre

, un arbre binomial

d'ordre

contenant les mêmes valeurs que celles des arbres a1 et a2. Dans la suite, on note a1

a2 cette opération.

Q9. Montrer par récurrence que la racine d'un arbre binomial d'ordre

a exactement

fils.
Q10. En déduire une fonction Python Ordre(a) qui renvoie l'ordre de l'arbre binomial a.
Q11. Montrer qu'un arbre binomial a d'ordre

possède

nœuds.
Q12. Écrire une fonction récursive Python EstUnArbreBinomial (a) qui renvoie True si a est un arbre binomial, False sinon.

II. 2 - Tas binomial

Un tas est une structure de données de type arbre qui permet en particulier de retrouver directement un élément qui doit être traité en priorité.

Définition 7 (Tas binomial)
Soient

un ensemble d'arbres. T est un tas binomial de longueur

si, pour tout

est soit un arbre vide, soit un arbre binomial d'ordre

. Si

ne peut, de plus, pas être vide et

est donc un arbre binomial d'ordre

On note dans la suite

le nombre de nœuds d'un tas T .
Q13. Quelle structure Python adopter pour coder un tas?
Définition 8 (Signature d'un tas)
Soit

un tas binomial de longueur

. On appelle signature de T la suite

telle que pour tout

(respectivement

) si l'arbre

est vide (respectivement n'est pas vide).

Q14. Soit T un tas binomial de longueur

. En utilisant sa signature, calculer

et montrer que

. En déduire

en fonction de

Q15. Écrire une fonction Python MinimumTas(T) qui retourne la valeur minimum du tas T. En donner la complexité en fonction de

Les tas se construisent itérativement à partir de données. On est donc amené, pour un tas T , à ajouter un à un des éléments.
Soit

un élément que l'on souhaite ajouter à un tas binomial T non vide et déjà construit. L'insertion de la valeur

dans le tas T se fait alors selon l'algorithme 1 .

Algorithme 1 - Insertion de $p$ dans T.
Entrées : un tas $\mathrm{T}=\left\{a_{0} \cdots a_{k}\right\}$, une valeur $p$
Sorties: un tas T augmenté de la valeur $p$
début
    $i \leftarrow 0$
    Coder $p$ dans un arbre binomial a d'ordre 0
    tant que $i<k+1$ et a non vide faire
        si $a_{i}$ est vide alors
            $a_{i} \leftarrow \mathrm{a}$
            Vider a
        sinon
            a $\quad a \oplus a_{i} \quad(* * *)$
            Vider $a_{i}$
        $i \leftarrow i+1$
    si a n'est pas vide alors
        Ajouter a au tas T.

Q16. Coder l'algorithme 1 sous la forme d'une fonction Python Insertion (

).
Q17. Évaluer la complexité de cet algorithme en fonction de

. On suppose que l'étape marquée (***) s'effectue en temps constant.

Q18. Donner la signature du tas résultant de l'insertion de

dans T en fonction de la signature de T .
Q19. Donner, sans justification, un invariant de boucle pour la boucle de l'algorithme 1 permettant de prouver la correction de ce dernier.

Partie III - Autour de l'énumération des fractions positives

Cette partie comporte des questions nécessitant un code OCaml. Pour ces questions, les réponses ne feront pas appel aux fonctionnalités impératives du langage (en particulier pas de boucles, pas de références).

Notations

Dans la suite, on notera:

le PGCD (Plus Grand Commun Diviseur) de et ;
la partie entière supérieure de x. Ainsi ;
la partie entière inférieure de x. Ainsi ;
la fonction logarithme de base 2. C'est la fonction réciproque de la fonction .

Une fraction, ou nombre rationnel, est le quotient de deux nombres entiers, le dénominateur étant par définition non nul. On notera

l'ensemble des fractions positives.
L'objectif de cette partie est d'étudier une structure de données permettant d'énumérer l'ensemble des fractions positives.

Plusieurs travaux se sont intéressés à l'énumération des nombres rationnels, le plus connu étant très certainement la méthode de Cantor. Cependant, il n'est très souvent pas possible, à moins d'un travail assez complexe, de connaître une formule générale donnant le

-ième terme de cette énumération, ni même de donner le successeur dans l'énumération d'une fraction donnée.
Nous proposons dans la suite de répondre à ces questions en construisant un arbre, dit de Calkin-Wilf, permettant de manipuler cette énumération.

Définition 9 (Arbre binaire infini)
Un arbre binaire homogène est un arbre binaire dont tous les nœuds ont 0 successeur ou 2 successeurs, appelés fils gauche et droit. La hauteur

de l'arbre est la profondeur maximale des nœuds de l'arbre, c'est-à-dire la plus grande longueur d'un chemin de la racine vers une feuille de l'arbre. Lorsque

est infinie, on parle d'arbre infini.

Définition 10 (Arbre de Calkin-Wilf)
L'arbre de Calkin-Wilf est un arbre binaire homogène infini dont les nœuds sont des fractions positives. La racine de l'arbre est la fraction

. Chaque sommet

a deux descendants : un fils gauche

et un fils droit

.
Ainsi, si

, les deux fils de

sont

(gauche) et

(droit).
Q20. Dessiner l'arbre de Calkin-Wilf jusqu'à une profondeur de 3. Par convention, la racine de l'arbre est au niveau 0.
On propose le type record :

pour définir une fraction de type

. La déclaration d'une telle fraction sera donc du type :

l'accès au numérateur (respectivement dénominateur) s'opérant par f.n; ; (resp. f.d; ; ).
Q21. Proposer un type OCaml récursif permettant de décrire l'arbre de Calkin-Wilf.
Q22. Montrer par récurrence sur le niveau d'exploration de l'arbre que si

est un nœud de l'arbre, alors

sont premiers entre eux.

Q23. Écrire une fonction récursive OCaml de signature pgcd : int * int -> int qui calcule le PGCD de deux entiers naturels.

Q24. Écrire une fonction récursive OCaml de signature fraction:int->int->fraction qui construit une fraction positive irréductible à partir d'un numérateur

et un dénominateur

. La fonction vérifie que

. Au besoin, elle simplifie la fraction par

Par la suite, on ne construira des valeurs de type fraction que par l'intermédiaire de la fonction fraction, ce qui permettra de garantir l'invariant de type suivant : "pour toute valeur

fraction,

sont premiers entre eux".

Q25. Soient deux nœuds

de l'arbre ayant des fils gauches (ou droits) identiques. Montrer qu'alors

Q26. Soient

un nœud et

. Montrer que le nœud provenant d'une suite de

fils gauches de

est le nœud

. Donner sans démonstration le nœud provenant d'une suite de

fils droits de

On définit alors une suite

, avec

, puis en effectuant un parcours en largeur, de gauche à droite, de l'arbre de Calkin-Wilf pour définir les termes de la suite.
Q27. Donner les huit premiers termes de la suite

Q28. Soient

premiers entre eux. Montrer par récurrence sur

que toute fraction

apparaît dans l'arbre.

Q29. Montrer qu'aucune fraction n'apparaît deux fois dans l'arbre.
Q30. Déduire des questions précédentes que la suite

est une bijection de

dans

.
La suite

permet donc d'affirmer que

est dénombrable. Nous allons utiliser

pour déterminer, dans l'énumération des fractions produite par cette suite, la position de n'importe quelle fraction positive

. En d'autres termes, étant donnée une fraction positive

, on se propose de rechercher

tel que

.
Q31. Soit

. Montrer que le fils gauche du nœud de valeur

a pour valeur

. Montrer de même que le fils droit a pour valeur

.
Pour pouvoir énoncer le i-ième terme dans cette énumération, on introduit alors une suite auxiliaire, aux nombreuses propriétés arithmétiques et liens avec d'autres objets mathématiques.

La suite diatomique de Stern (ou suite de Stern-Brocot) doit son nom à Moritz Stern (1807-1894), élève de Gauss et Achille Brocot (1817-1878), horloger qui s'intéressait aux fractions pour la fabrication d'horloges avec des engrenages comportant peu de dents, donc simples à fabriquer.

Définition 11 (Suite diatomique de Stern ou suite de Stern-Brocot)
La suite diatomique de Stern

est définie par

et pour tout

Q32. Donner les dix premiers termes de la suite

.
Q33. Écrire une fonction récursive OCaml de signature stern : int -> int permettant de calculer les termes de cette suite.

Q34. Déduire par récurrence de la Q31 que :

.
La suite diatomique de Stern permet d'exprimer le i-ième terme dans l'énumération des fractions positives qui est induite par le parcours en largeur de l'arbre de Calkin-Wilf décrit ci-dessus.

Voyons maintenant comment obtenir de manière rapide le successeur d'une fraction

donnée, sans connaître

, dans cette énumération. Trois cas peuvent se présenter :

premier cas : les nœuds de valeur et sont à même profondeur , fils d'un même nœud ,
deuxième cas : le nœud de valeur est le dernier nœud à droite à la profondeur ,
troisième cas : les nœuds de valeur et sont à même profondeur , mais ne sont pas fils d'un même nœud.
On pose pour tout .
Q35. Montrer que dans le premier cas, .
Q36. Montrer, en utilisant la Q26, que dans le deuxième cas on a encore .
On étudie enfin le dernier cas : les nœuds de valeur et sont sur une même profondeur , mais ne sont pas les fils d'un même nœud. On va donc passer par la recherche d'un ancêtre commun de ces deux nœuds. Dans la suite, on s'intéressera toujours au premier ancêtre commun, c'est-à-dire celui de profondeur maximale.
En partant de la racine r , il est possible d'atteindre n'importe quel nœud de l'arbre par une suite de déplacements vers la gauche (G) ou vers la droite (D). Le chemin de r vers peut donc être codé par un mot sur l'alphabet {G,D}.

Si un déplacement est représenté en OCaml par un type

alors un chemin est une liste direction list.
Q37. Écrire une fonction OCaml de signature chemin : fraction -> direction list qui calcule le chemin de la racine à un nœud quelconque de l'arbre. Cette fonction fera appel à une fonction auxiliaire récursive. Ainsi chemin n d calcule la liste des directions à prendre pour passer de r au nœud

. On pourra supposer l'existence d'une fonction de signature rev : direction list -> direction list qui renverse une liste.

Q38. Écrire une fonction OCaml de signature noeud : direction list -> fraction qui détermine le nœud obtenu en effectuant une série de déplacements depuis la racine. Ainsi noeud

renverra un couple d'entiers (

) correspondant au nœud de valeur

. Cette fonction fera appel à une fonction auxiliaire récursive.

Q39. Utiliser les deux fonctions précédentes pour écrire une fonction OCaml ancetre de signature ancetre : fraction -> fraction -> fraction qui détermine le premier ancêtre commun entre deux nœuds. Ainsi ancetre (

) (

) détermine le premier ancêtre commun à

. Cette fonction pourra utiliser une fonction auxiliaire récursive.

Q40. On suppose que le nœud de valeur

, le premier ancêtre commun des nœuds de valeur

, est à

niveaux au-dessus d'eux. Donner le chemin entre

sous la forme d'une liste de direction. Donner de même le chemin entre

Q41. À partir de l'expression des fils gauche et droit de

, montrer que l'on a encore