J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

CCINP Option Informatique MP 2021

Partitions non croisées, problème Horn-Sat, classes sylvestres

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ccinp
🔗 Explorer
Banque
CCINP
Année
2021
Filière
MP
Matière
Info
CCINP MPCCINP 2021MP InfoInfo 2021
2025_08_29_52cabc7c1e667762251dg

ÉPREUVE MUTUALISÉE AVEC E3A-POLYTECH ÉPREUVE SPÉCIFIQUE - FILIÈRE MP

INFORMATIQUE

Durée : 4 heures
N.B. : le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

RAPPEL DES CONSIGNES

  • Utiliser uniquement un stylo noir ou bleu foncé non effaçable pour la rédaction de votre composition ; d'autres couleurs, excepté le vert, peuvent être utilisées, mais exclusivement pour les schémas et la mise en évidence des résultats.
  • Ne pas utiliser de correcteur.
  • Écrire le mot FIN à la fin de votre composition.

Les calculatrices sont interdites.

Le sujet est composé de trois parties indépendantes.

Partie I - Étude des partitions non croisées

Dans cette partie, on introduit et on étudie de façon élémentaire les partitions non croisées, objets combinatoires apparaissant dans divers domaines des mathématiques, notamment dans la théorie des probabilités libres et des matrices aléatoires.
Le langage de programmation utilisé dans cette partie est le langage Python.
Dans la suite, pour tout couple , les notations et désignent respectivement les ensembles et . Par convention, et si alors .
Définition 1 (Partition)
Soit un sous-ensemble non vide de . Une partition de est un ensemble de parties de tel que :
  1. ;
  2. ;
  3. .
Par exemple, est une partition de l'ensemble .
Définition 2 (Classe)
Soit une partition d'un sous-ensemble non vide de . Soit un élément de . La classe de est l'unique élément de tel que . Elle est notée .
Par exemple, pour , on a .
Définition 3 (Partition non croisée)
Soit une partition d'un sous-ensemble non vide de . On dit que est non croisée si pour tout quadruplet tel que on a :
Par exemple, est bien une partition non croisée de . En effet, aucun quadruplet tel que ne vérifie la condition .
De même, en est bien une. En effet, est l'unique quadruplet tel que vérifiant et ces quatre éléments sont bien dans la même classe.
Par contre, n'en est pas une. En effet, et mais .
Le terme «non croisée» découle naturellement des représentations picturales des partitions (figure 1).
Figure 1 - Représentations picturales de
Dans la suite, on s'intéresse uniquement aux partitions d'un sous-ensemble fini de . On les représente en Python à l'aide de listes de listes croissantes d'entiers triées dans l'ordre lexicographique.
Par exemple, les partitions et sont respectivement représentées par les listes et .

I. 1 - Exemples et fonctions élémentaires (Informatique Pour Tous)

Q1. Justifier brièvement que est une partition non croisée de et que n'en est pas une.
Q2. Parmi les ensembles suivants, indiquer sans justification lesquels sont des partitions de . Parmi les partitions, préciser sans justification lesquelles sont non croisées.
  1. ,
  2. ,
  3. ,
  4. .
Q3. Décrire l'ensemble des partitions non croisées de [4]].
Pour Q4, Q5 et Q6, on se fixe un ensemble fini . Cet ensemble est représenté en Python par la liste croissante d'entiers A , définie au préalable. On suppose également que pour ces questions, la variable P désigne une liste de listes croissantes d'entiers triée dans l'ordre lexicographique.
On définit la fonction Python mystere(P) par :
def mystere(P) :
    L = [False for _ in range(len(A))]
    for i in range(len(P)) :
        if P[i] == [] :
            return False
        else :
            for j in range(len(P[i])) :
                if P[i][j] not in A :
                    return False
                else :
                    # A.index(a) renvoie l'indice de a dans A
                    k = A.index(P[i][j])
                    if L[k] :
                        return False
                    else:
                        L[k] = True
    return not (False in L)
Q4. Uniquement dans cette question, on suppose que .
Expliciter sans justification les valeurs de :
1. mystere([[1,3],[1,5],[2,4]]) 2. mystere([[1,3,4],[2]])
3. mystere([[1,3,5],[2,4]]) 4. mystere([[],[1,2,3,4,5]]).
Q5. Écrire une fonction Python classe( ) prenant en arguments une variable P représentant une partition de et un entier qui renvoie une liste représentant .
On définit la fonction Python au code incomplet est_nc(P) suivante :
def est_nc(P) :
    # On rappelle que A est une liste triée dans l'ordre croissant
    N = len(A)
    for i in range(N) :
        for j in range ( }\textrm{i}+1,\textrm{N}\mathrm{ ) :
            for k in range( j + 1,N) :
                for l in range ( }\textrm{k}+1,\textrm{N}\mathrm{ ) :
Q6. Recopier et compléter le code de la fonction est_nc (P), sachant qu'elle prend en argument une variable P représentant une partition de et qu'elle renvoie True si est non croisée et False sinon.

I. 2 - Nombre de partitions non croisées

Pour tout , on note le nombre de partitions non croisées d'un ensemble ayant exactement éléments et l'ensemble des partitions non croisées de . Par convention, et .
Définition 4 (Partition non croisée emboîtée)
Soient un ensemble fini de de cardinal et une partition non croisée de . On dit que est emboîtée si le minimum et le maximum de sont dans la même classe ( ). L'ensemble des partitions non croisées et emboîtées de et son cardinal sont respectivement notés et .
Par exemple, est une partition non croisée et emboîtée de .
Le terme «emboîtée» découle naturellement des représentations picturales des partitions (figure 2).
Figure 2 - Représentations picturale de
Q7. Montrer que pour tout , on a .
Q8. Soit . On définit l'application comme suit :
En admettant que est une application bijective, montrer que .
Q9. (Informatique Pour Tous) Écrire une fonction Python calcul_C(n) qui prend en argument un entier naturel n et qui renvoie la valeur .

Partie II - Logique et étude du problème Horn-Sat

Dans cette partie, , désignent respectivement les connecteurs de conjonction, de disjonction et de négation. Les symboles désignent respectivement les valeurs de vérité VRAI et FAUX du calcul propositionnel.
Dans la suite, on s'intéresse au problème Horn-Sat, qui peut être décrit de la façon suivante : étant donnée une formule de Horn , existe-t-il une interprétation telle que ?
L'objectif est d'expliciter un algorithme permettant de résoudre ce problème.
Définition 5 (Formule propositionnelle)
Soit un ensemble de symboles appelés variables propositionnelles. Les formules propositionnelles sur sont alors définies de façon inductive comme suit :
  • V, F sont des formules propositionnelles;
  • tout élément de est une formule propositionnelle;
  • si et sont des formules propositionnelles, alors sont des formules propositionnelles.
Dans la suite, les variables propositionnelles et formules propositionnelles considérées sont construites à l'aide d'un ensemble qui ne sera pas explicité.
Définition 6 (Littéral)
Soit une variable propositionnelle. Un littéral est la formule ou la formule . Le littéral (respectivement ) est un littéral positif (respectivement négatif).
Définition 7 (Clause disjonctive)
Soient des littéraux. La formule est appelée clause disjonctive à littéraux (ou de taille ). Par convention, () désigne la clause disjonctive vide, c'est-à-dire la clause sans littéral.
Une clause de Horn est une clause disjonctive contenant au plus un littéral positif.
Une clause unitaire est une clause composée d'un unique littéral.
Définition 8 (Forme normale conjonctive)
Soit une formule propositionnelle. On dit que est une forme normale conjonctive s'il existe un entier des clauses disjonctives vérifiant . Par convention, une forme normale conjonctive sans clause est représentée par .
Définition 9 (formule de Horn)
Soit une formule propositionnelle. On dit que est une formule de Horn s'il existe des clauses de Horn vérifiant .
Définition 10 (Interprétation)
Soient et des variables propositionnelles. Une interprétation est une application .
Définition 11 (Évaluation)
Soient une formule propositionnelle, les variables propositionnelles apparaissant dans et une interprétation sur . L'évaluation de suivant l'interprétation que l'on note est définie par récurrence de la façon suivante :
  • si , alors ;
  • si , alors ;
  • si où est une formule propositionnelle, alors ;
  • si où sont des formules propositionnelles et , alors .
Par convention, et .
Définition 12 (Satisfiable)
Soit une formule propositionnelle. On dit que est satisfiable s'il existe une interprétation telle que .
Q10. Pour chacune des formules suivantes, montrer qu'elle est satisfiable ou qu'elle est non satisfiable.
  1. ,
  2. ,
  3. ,
  4. .
Q11. Parmi les fomules de la Q10, lesquelles sont des formules de Horn? On ne justifiera pas la réponse.
Définition 13 (Propagation unitaire)
Soit une forme normale conjonctive contenant une clause unitaire . On construit une formule à partir de de la façon suivante :
  1. supprimer de toutes les clauses où apparaît;
  2. enlever toutes les occurrences du littéral .
Cette procédure de simplification est appelée propagation unitaire.
Par exemple, si , on a alors . Si , on a alors .
Dans la suite, on note une formule sans clause unitaire obtenue en itérant la propagation unitaire sur . On admet que si ne contient pas de clause vide () alors est unique et que si contient au moins une clause vide alors toute formule sans clause unitaire obtenue par itération de la propagation unitaire sur contient au moins une clause vide.
Q12. On pose :
Calculer . On pourra donner le résultat directement sans détailler les calculs.
Q13. Soit une formule de Horn. Montrer que est une formule de Horn.
Q14. Soit une forme normale conjonctive. Montrer que est satisfiable si et seulement si est satisfiable.
Q15. Soit une forme normale conjonctive. Montrer que si () apparaît dans , alors n'est pas satisfiable.
Q16. Soit une clause de Horn. Montrer que si n'est ni la clause vide ni une clause unitaire positive, alors est satisfiable.
Q17. Soit une formule de Horn ne contenant ni de clause vide ni de clause unitaire positive. Montrer que est satisfiable.
Q18. Soit une formule de Horn. Montrer que n'est pas satisfiable si et seulement si () apparaît dans .

Partie III - Étude des classes sylvestres

Étant donné un arbre binaire de recherche , sa classe sylvestre est l'ensemble des mots qui donnent l'arbre après insertion dans l'arbre vide. L'objectif de cette partie est de donner une caractérisation et une description de cet ensemble. On commence par rappeler la structure des arbres binaires de recherche ainsi que leurs propriétés usuelles. Puis, on introduit la notion de S -équivalence sur les mots qui permet de caractériser la classe sylvestre d'un arbre . Enfin, à l'aide du produit de mélange, on présente un algorithme calculant la classe sylvestre d'un arbre donné.
Dans toute la suite, désigne un alphabet fini totalement ordonné. Le symbole désigne le mot vide.

III. 1 - Algorithme d'insertion dans un arbre binaire

Définition 14 (Arbre binaire)
Un arbre binaire (étiqueté par les éléments de ) est récursivement soit :
  • l'arbre vide que l'on note ;
  • un triplet ( ) où est un élément de et des arbres binaires. Les éléments et sont respectivement appelés racine, sous-arbre gauche et sous-arbre droit de .
Définition 15 (Arbre binaire de recherche)
Un Arbre Binaire de Recherche (abrégé en ABR) est récursivement soit :
  • l'arbre vide;
  • un triplet ( ) où est un élément de et des ABR. De plus, toute valeur apparaissant dans est strictement inférieure à et toute valeur apparaissant dans est supérieure ou égale à .
Définition 16 (Insertion dans un arbre binaire)
L'insertion d'un élément de dans un arbre binaire est une opération que l'on note définie récursivement comme suit :
  • si , alors ;
  • si et , alors ;
  • si et , alors .
On définit récursivement alors l'insertion d'un mot dans un arbre binaire noté également comme suit :
  • si , alors
  • si avec , alors .
Dans le cas où est un , on admet que et sont également des ABR.
Étant donné un mot sur , l'arbre binaire de recherche associé à est l'arbre .
Définition 17 (Classe sylvestre)
Soit un arbre binaire de recherche. La classe sylvestre de que l'on note est l'ensemble des mots vérifiant : .
Par exemple, si , on a .
Et si , alors .
Pour simplifier la représentation des arbres binaires, on peut utiliser des graphes.
Par exemple, l'arbre est représenté dans la figure 3.
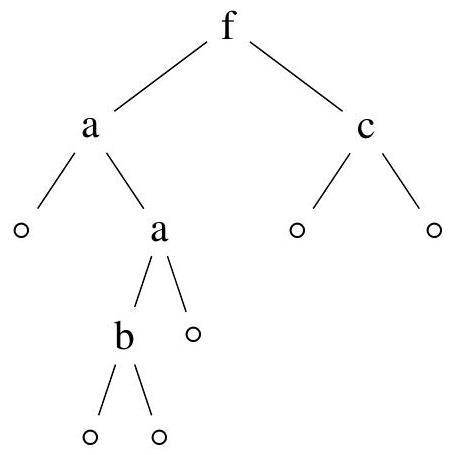
Figure 3 - Représentation de
Dans la suite, les lettres de sont représentées en Ocaml par des char et les mots sur l'alphabet par des char list. Ainsi, le mot "arbre" est représenté par la liste ' a ' ' r ' ; ' b ' ; ' r ' ; ' e ' . On représente les arbres binaires en Ocaml à l'aide de la structure arbre suivante :
type 'a arbre = Vide | Noeud of ('a arbre) * 'a * ('a arbre).
Ainsi, l'arbre est représenté en Ocaml par:
Noeud(Vide, 'a', Noeud(Vide, 'b', Vide)).
Q19. Représenter le graphe de l'ABR associé au mot "fantastique", l'ordre sur les lettres étant l'ordre alphabétique.
Q20. Écrire une fonction récursive en Ocaml de signature :
insertion_lettre : char -> char arbre -> char arbre
et telle que insertion_lettre a t est l'arbre binaire obtenu en insérant la lettre a dans l'arbre binaire t .
Q21. Écrire une fonction récursive en Ocaml de signature :
insertion_mot : char list -> char arbre -> char arbre
et telle que insertion_mot w t est l'arbre binaire obtenu en insérant le mot w dans l'arbre binaire t .
Définition 18 (Lecture préfixe)
Soit un arbre binaire. La lecture préfixe de que l'on note est le mot défini récursivement par :
  • si , alors ;
  • si , alors où et sont les lectures préfixes respectives de et de .
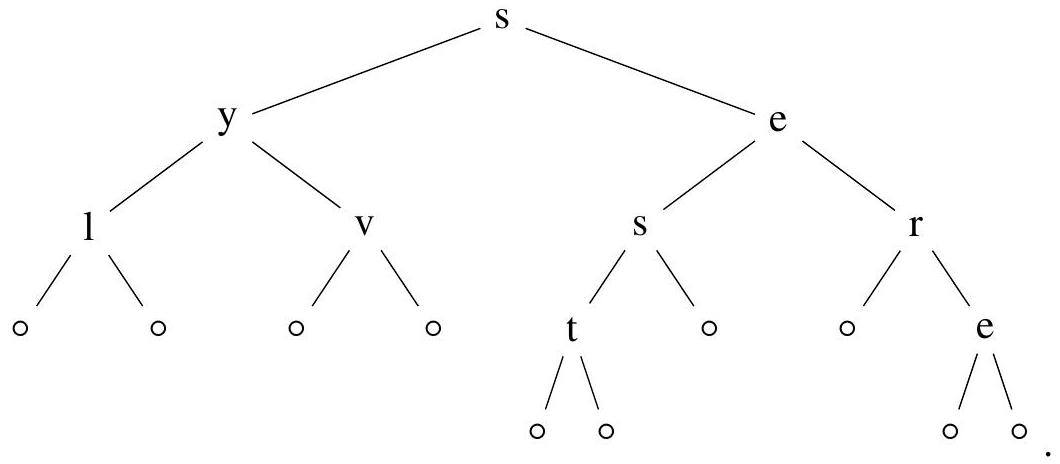
Q22. Expliciter pour l'arbre binaire représenté ci-dessous :
Figure 4 - Représentation de de Q22
Q23. Écrire une fonction récursive en Ocaml de signature :
prefixe : char arbre -> char list
et telle que prefixe est le mot qui correspond à la lecture préfixe de l'arbre .
Q24. Soit un , soit la lecture préfixe de . Montrer que est l'ABR associé à .

III. 2 - Une relation d'équivalence sur les mots

Définition 19 (S-adjacence)
Soient et deux mots sur . On dit que est -adjacent à (ou que et sont S -adjacents) s'il existe trois lettres de et trois mots sur vérifiant:
Définition 20 (S-équivalence)
Soient et deux mots sur . On dit que est S -équivalent à (ou que et sont S-équivalents) s'il existe vérifiant :
à
Q25. Montrer que la relation " être -équivalent à " est bien une relation d'équivalence sur .
Q26. Soient trois lettres de vérifiant . Montrer que pour tout arbre binaire de recherche contenant au moins la lettre , on a : . On pourra raisonner par récurrence sur le nombre de nœuds de .
Q27. Montrer que si deux mots et sont S-équivalents, alors les ABR et sont égaux.
Q28. Soit un mot de longueur sur , soit la première lettre de . On veut montrer qu'il existe un mot où (respectivement ) est un mot dont toutes les lettres sont plus petites strictement (respectivement plus grandes au sens large) que et tels que et sont S -équivalents. On note l'ensemble des mots S -équivalents à .
Pour tout , on pose :
(a) Justifier que l'ensemble est fini.
(b) Justifier que tous les mots de commencent par .
(c) Soit . Montrer que si , alors il existe tel que .
(d) Soit . Montrer que si , alors il existe (respectivement ) un mot dont toutes les lettres sont plus petites strictes (respectivement plus grandes ou égales) que et tels que .
(e) Soit un élément de tel que le nombre d'éléments de soit le plus petit possible. Montrer par l'absurde que et en déduire qu'il existe vérifiant les conditions de la question tels que ruv et sont S-équivalents.
Q29. Montrer que tout mot est S-équivalent à , où est la lecture préfixe de . On pourra raisonner par récurrence sur la longueur du mot et exploiter les résultats de la .
Q30. En déduire que deux mots sont S -équivalents si et seulement si ils sont des éléments d'une même classe sylvestre.

III. 3 - Construction de classes sylvestres

Pour construire des classes sylvestres, il est utile d'utiliser le produit de mélange.

Définition 21 (Mélange)

Soient et deux mots sur . Le mélange de et , noté , est l'ensemble récursivement défini comme suit :
  • si , alors
  • si , alors ;
  • si et où et sont des lettres, et des mots, alors :
Définition 22 (Mélange de langages)
Soient et deux langages. Le mélange des langages et , noté , est défini par :
Si au moins un des deux langages est égal à l'ensemble , alors on a .
Étant donné un , on peut montrer que :
On admet ce résultat pour la suite de cette sous-partie. On note que .
Q31. Expliciter sans justification tous les éléments de l'ensemble .
Q32. Écrire une fonction récursive en Ocaml de signature :
ajout_lettre : char -> char list list -> char list list
et telle que ajout_lettre a liste est la liste de mots de la forme où w est un élément de liste.
Q33. Écrire une fonction récursive en Ocaml de signature :
shuffle : char list-> char list -> char list list
et telle que shuffle est une liste contenant exactement tous les mots de avec répétitions possibles d'un même mot. On devra utiliser la fonction auxiliaire ajout_lettre et l'opérateur de concaténation @.
Q34. Écrire une fonction récursive en Ocaml de signature :
shuffle_l : char list list -> char list list -> char list list
et telle que shuffle_l l m est une liste contenant exactement tous les mots de où la liste 1 (respectivement m ) représente le langage (respectivement ), avec répétitions possibles d'un même mot. Seules les fonctions définies précédemment peuvent être utilisées en fonctions auxiliaires.
Q35. Écrire une fonction récursive en Ocaml de signature :
sylvestre_T : char arbre -> char list list
et telle que sylvestre_T t est une liste contenant exactement tous les éléments de la classe sylvestre de t . Seules les fonctions définies précédemment peuvent être utilisées en fonctions auxiliaires.

FIN

CCINP Option Informatique MP 2021 - Version Web LaTeX | WikiPrépa | WikiPrépa