J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

CCINP Modélisation TPC 2020

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ccinp
🔗 Explorer
Banque
CCINP
Année
2020
Filière
TPC
Matière
Modelisation
CCINP TPCCCINP 2020TPC ModelisationModelisation 2020
2025_09_04_c962ab34e76aead58e23g

ÉPREUVE SPÉCIFIQUE - FILIÈRE TPC

MODÉLISATION

Mercredi 6 mai : 8 h - 12 h

N.B. : le candidat attachera la plus grande importance à la clarté, à la précision et à la concision de la rédaction. Si un candidat est amené à repérer ce qui peut lui sembler être une erreur d'énoncé, il le signalera sur sa copie et devra poursuivre sa composition en expliquant les raisons des initiatives qu'il a été amené à prendre.

RAPPEL DES CONSIGNES

  • Utiliser uniquement un stylo noir ou bleu foncé non effaçable pour la rédaction de votre composition ; d'autres couleurs, excepté le vert, peuvent être utilisées, mais exclusivement pour les schémas et la mise en évidence des résultats.
  • Ne pas utiliser de correcteur.
  • Écrire le mot FIN à la fin de votre composition.

Les calculatrices sont autorisées.

Le sujet est composé de deux parties (pages 1 à 11)
et d'une annexe (page 12).

Calcul de la contribution de la rotation interne du groupe méthyle à l'entropie de la molécule d'éthane

Présentation du problème

Le calcul des propriétés chimiques de systèmes moléculaires est aujourd'hui facilité par le développement de logiciels basés sur les lois fondamentales de la mécanique quantique. Ce type de logiciels permet par exemple de trouver la géométrie pour laquelle l'énergie d'une molécule est minimale, de calculer son énergie et ses fréquences de vibration.
Même si la plupart des étapes de calcul des données thermodynamiques des molécules sont automatisées, il est parfois nécessaire de réaliser des corrections manuellement pour obtenir des valeurs en accord avec l'expérience.
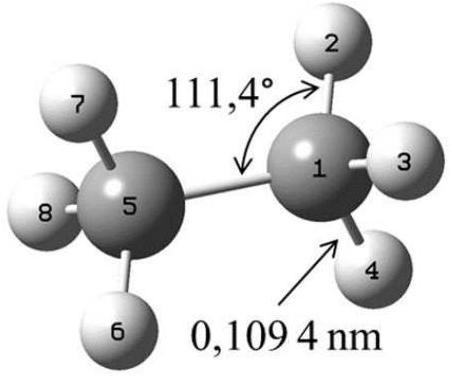
C'est le cas lorsque l'on souhaite calculer précisément la valeur de l'entropie d'une molécule qui possède des groupes méthyle. Une des molécules se trouvant dans ce cas est la molécule d'éthane dont la structure est représentée sur la figure 1.
Figure 1 - Structure de la molécule d'éthane
La rotation du groupe méthyle autour de la liaison entre les deux atomes de carbone peut être représentée par différents modèles simples. Le choix du modèle dépend de la hauteur de la barrière d'énergie potentielle à franchir lors de la rotation du groupe méthyle autour de la liaison entre les deux atomes de carbone. Parmi ces modèles, on trouve celui de la rotation libre, le modèle de l'oscillateur harmonique angulaire et le modèle de la rotation empêchée.
La première partie de l'épreuve concerne l'étude des conformations de l'éthane. Une attention particulière est portée aux informations que l'on peut tirer de l'évolution de l'énergie potentielle associée à la rotation du groupe méthyle. La partie suivante est relative au calcul de la contribution de la rotation interne du groupe méthyle à l'entropie de la molécule d'éthane en considérant différents modèles pour représenter la rotation.

Partie I - Étude des conformations de la molécule d'éthane

Q1. Rappeler à quel type d'isomérie s'apparentent des espèces dont la structure diffère par la rotation autour des liaisons simples. Rappeler le nom que l'on donne à ce type d'isomères.
On s'intéresse à la molécule d'éthane ( , voir figure 1) dont l'ensemble des conformations est obtenu par rotation des deux groupes méthyle autour de la liaison simple entre les deux atomes de carbone.
Q2. Donner les projections de Cram et de Newman correspondant aux deux conformations remarquables dites décalée et éclipsée, en précisant clairement de laquelle il s'agit.
Le graphe de la figure 2 montre l'évolution sinusoïdale de l'énergie potentielle d'un groupe méthyle par rapport à l'autre supposé fixe, en fonction de l'angle de rotation autour de la liaison de la molécule d'éthane.
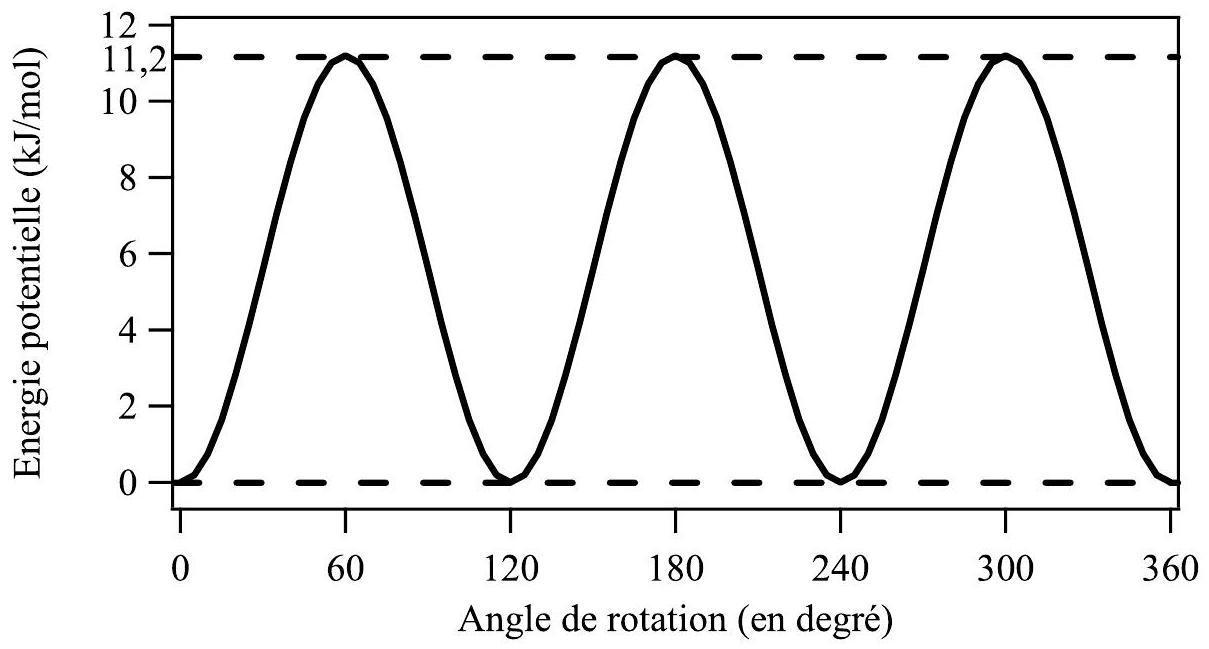
Figure 2 - Évolution de l'énergie potentielle associée à la rotation d'un groupe méthyle de la molécule d'éthane en fonction de l'angle de rotation
Q3. Indiquer à quelles conformations correspondent les minima et maxima observés sur la courbe. Expliquer brièvement l'origine de la variation de l'énergie potentielle de la molécule d'éthane en fonction de l'angle de rotation.
Le passage d'une conformation stable à l'autre nécessite le franchissement d'une barrière d'énergie potentielle qui sera notée . En raison de la symétrie du groupe méthyle, on constate que cette barrière est franchie plusieurs fois de manière périodique lors d'un tour complet.
Q4. En analysant le graphe de la figure 2, relever la valeur de la barrière d'énergie potentielle .

Partie II - Contribution de la rotation interne du groupe méthyle à l'entropie de la molécule d'éthane

Comme indiqué dans l'introduction, la rotation interne du groupe méthyle par rapport au second apporte une contribution à l'entropie de la molécule d'éthane. Le calcul de cette contribution dépend du type de rotation considérée. On distingue deux cas selon la valeur de l'énergie potentielle :
  • si , la rotation est libre;
  • si , la rotation est empêchée,
    où est la constante des gaz parfaits et la température.
    Q5. Préciser quel type de rotation est observé selon que l'on se trouve à très basse température, 100 K , ou à très haute température, 2000 K .

II. 1 - Calcul de la contribution à l'entropie pour une rotation libre

Dans le cas d'une rotation libre de la molécule d'éthane, on peut montrer que la contribution à l'entropie s'écrit :
avec la constante des gaz parfaits, la constante de Planck, la constante de Boltzmann et le moment d'inertie du groupe méthyle en rotation autour de l'axe matérialisé par la liaison entre les deux atomes de carbone de la molécule d'éthane. Le moment d'inertie s'écrit :
avec la masse de l'atome d'hydrogène et la distance entre l'atome et sa projection orthogonale sur l'axe de rotation joignant les deux carbones.
Q6. Calculer, dans les unités du Système International, le moment d'inertie d'un groupe méthyle (visible sur la figure 1) à partir des données suivantes :
  • masse d'un atome d'hydrogène :
  • longueur des liaisons
  • valeur des angles
Q7. Calculer la contribution à l'entropie dans le cas de la rotation libre à dans les unités du Système International avec un nombre adéquat de chiffres significatifs.
Données : et .

II. 2 - Calcul de la contribution à l'entropie pour un oscillateur harmonique

Dans le cas de la rotation empêchée, le modèle de l'oscillateur harmonique permet d'estimer la contribution de la rotation du groupe méthyle à l'entropie de la molécule d'éthane, comme en témoigne le tracé des énergies potentielles correspondantes sur le graphe de la figure 3.
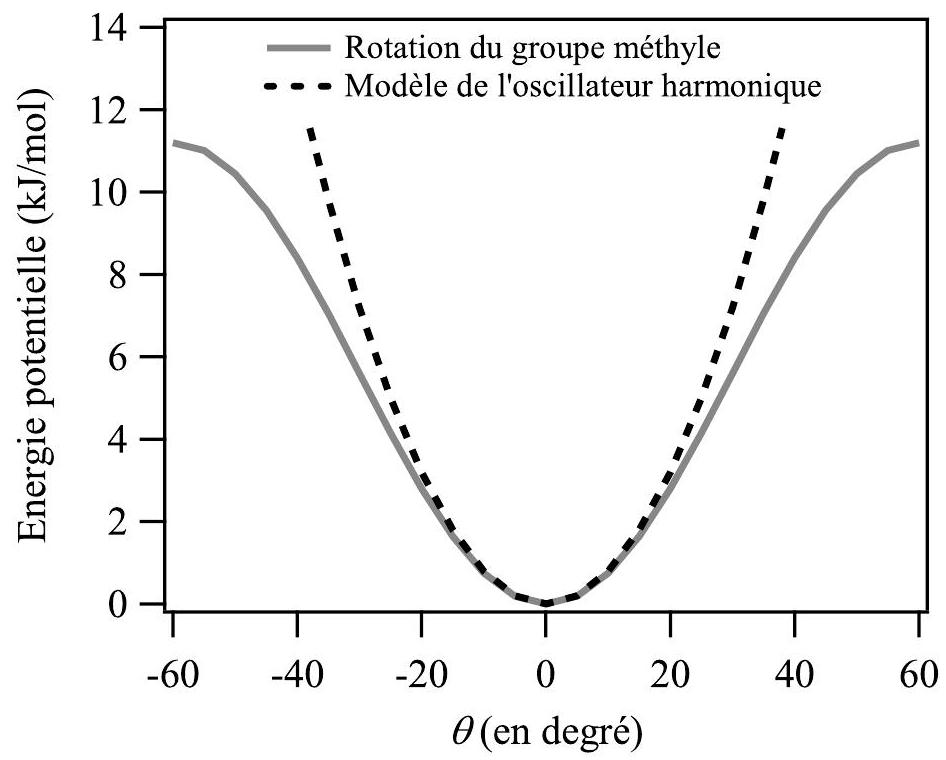
Figure 3 - Approximation de la rotation interne du groupe méthyle par le modèle de l'oscillateur harmonique

Traitement quantique de l'oscillateur harmonique

La détermination de la contribution de la rotation du groupe méthyle à l'entropie de la molécule d'éthane peut se faire en résolvant l'équation de Schrödinger unidimensionnelle stationnaire dans le cas de l'oscillateur harmonique. La fonction d'onde étudiée est celle du proton de l'atome d'hydrogène placé dans le puits de potentiel harmonique associé à la rotation interne du groupe méthyle. On note :
l'énergie potentielle à laquelle est soumise l'atome d'hydrogène lors de la rotation d'angle du groupe méthyle autour de la liaison , où est une constante.
L'équation de Schrödinger stationnaire en coordonnées cylindriques peut se mettre sous la forme :
avec la masse d'un atome d'hydrogène, la constante de Planck réduite, la fonction d'onde associée à un état propre, la valeur propre correspondante et l'énergie potentielle à laquelle est soumise l'atome d'hydrogène. Les énergies et sont exprimées en joule.
En coordonnées cylindriques, le laplacien de la fonction d'onde s'écrit :
Q8. La mise en équation du problème permettant de supposer les variables et constantes, proposer une expression simplifiée du laplacien .
Réécrire alors l'équation de Schrödinger sous la forme et donner l'expression de l'opérateur .
Pour simplifier la résolution de cette équation, on la réécrit sous la forme adimensionnelle suivante :
où est un paramètre dont nous allons établir l'expression et est appelée l'abscisse réduite avec la pulsation propre de l'oscillateur.
Q9. Déterminer la dimension de l'abscisse réduite .
Q10. Déduire de la question Q8 et de l'équation (6), l'expression du paramètre en fonction de et et vérifier qu'il est sans dimension.

Résolution numérique par la méthode de Numerov

Nous allons résoudre numériquement l'équation (6) pour trouver les valeurs de pour le niveau d'énergie par la méthode de Numerov. Il s'agit d'une méthode permettant de réaliser l'intégration de certains types d'équations différentielles, dont celles de la forme :
Q11. Donner les expressions des fonctions et en procédant par identification entre les équations (6) et (7).
La résolution de l'équation différentielle (7) passe par sa discrétisation. Pour ce faire, l'intervalle des abscisses est divisé en un nombre fini de points régulièrement espacés de , le pas d'espace. On utilise l'indice pour repérer ces différents points, d'abscisse discrétisée . On exprime la fonction d'onde en et ses voisins à l'aide des notations et . Le pas est suffisamment petit pour que l'on puisse écrire et .
Q12. En écrivant le développement limité de et de à un ordre suffisant, établir l'expression:
Pour simplifier l'écriture, on pose .
Q13. En effectuant un développement limité à l'ordre 2 des fonctions et , montrer que :
Comme pour la fonction , on note et .
Q14. Réécrire l'équation (7) à l'aide uniquement de et .
L'équation (8) peut se mettre sous la forme factorisée suivante :
Q15. En posant , démontrer à partir de l'équation (10) la relation de récurrence :
Pour résoudre numériquement l'équation (7), on prendra où est le paramètre dont l'expression est établie à la question Q10.

Algorithme général de résolution du problème

La résolution doit nous permettre d'obtenir la fonction d'onde et l'énergie réduite de l'état quantique caractérisé par l'entier positif ou nul .
Lors de la résolution numérique, il ne faut conserver que les fonctions d'onde compatibles avec les conditions aux limites du problème. Pour cela, on compte le nombre de zéros de la fonction d'onde (c'est-à-dire le nombre de points d'intersection de la fonction d'onde avec l'axe des abscisses) que l'on appelle des nœuds et on vérifie qu'il correspond à la valeur attendue pour l'état quantique caractérisé par l'entier .
Q16. À partir de l'allure des premiers termes de la fonction d'onde , représentée sur la figure 4, donner la relation entre et le nombre de nœuds de la fonction d'onde .
On admettra ensuite la généralité de cette relation.
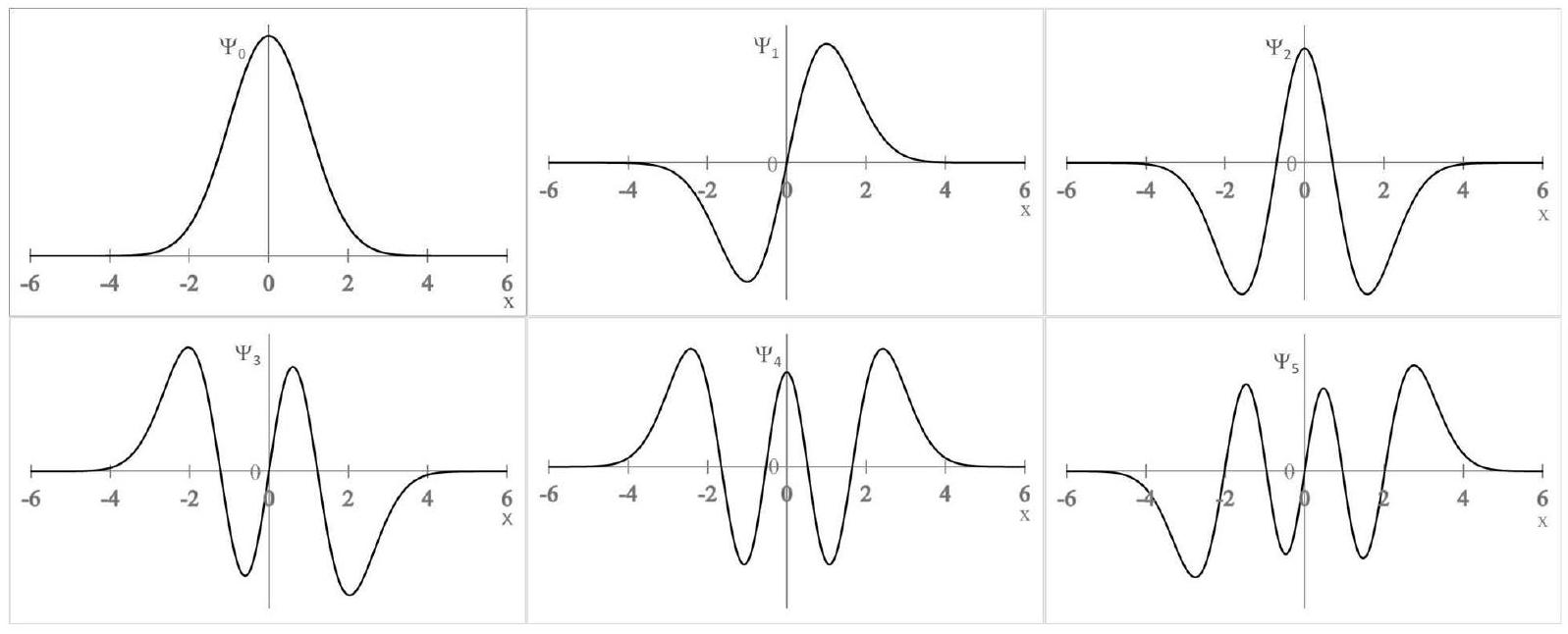
Figure 4 - Allure des fonctions d'onde associées aux premiers niveaux d'énergie de l'oscillateur harmonique quantique unidimensionnel
Q17. Justifier, à partir de l'allure des courbes de la figure 4, qu'il est possible de restreindre l'intervalle d'intégration aux seules valeurs positives de . Donner la relation entre et selon la parité de .
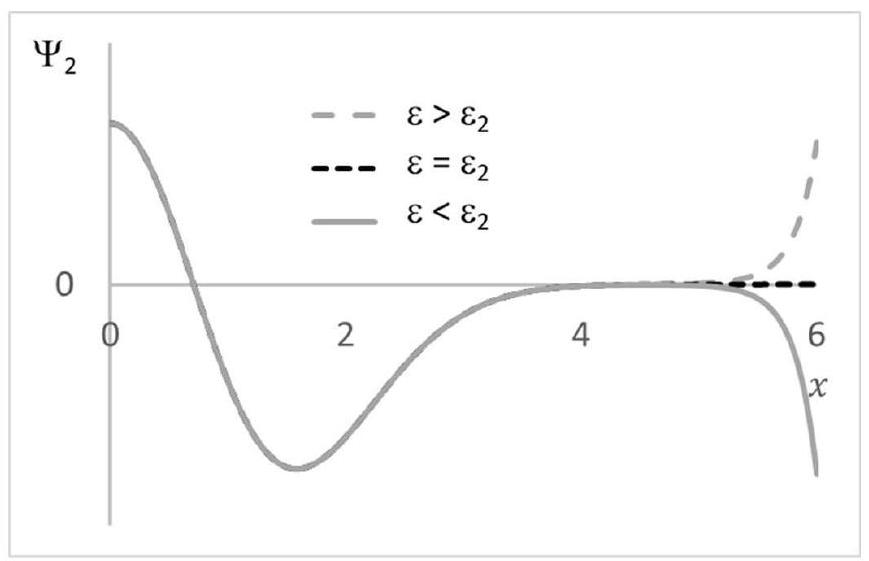
Le graphe de la figure 5 illustre, dans le cas , ce que l'on obtient lors de la résolution numérique de l'équation de Schrödinger pour une énergie réduite inférieure, égale ou supérieure à la valeur propre . Lorsque , on observe que la fonction d'onde diverge au lieu de tendre vers 0 quand on s'éloigne de l'origine.
Figure 5 - Allures de la fonction d'onde sur l'intervalle positif pour la valeur propre , pour une énergie réduite inférieure, égale ou supérieure à . Les trois courbes coïncident jusque vers .
Q18. Dans le cas où , que remarque-t-on concernant le nombre de nœuds de la fonction d'onde? Dans la suite, on supposera que cette observation est valable pour tout .
L'algorithme général de résolution du problème par une méthode dichotomique est le suivant :
- Initialisation de n
- Initialisation des valeurs limites de }\varepsilon(\mp@subsup{\varepsilon}{\operatorname{min}}{}\mathrm{ et }\mp@subsup{\varepsilon}{\operatorname{max}}{})\mathrm{ qui encadrent }\mp@subsup{\varepsilon}{n}{
- Début de la boucle conditionnelle si le critère de convergence n'est pas satisfait
    - Actualisation de }\varepsilon=(\mp@subsup{\varepsilon}{\operatorname{min}}{}+\mp@subsup{\varepsilon}{\operatorname{max}}{})/2\mathrm{ (la dichotomie)
    - Appel des fonctions permettant de résoudre l'équation de Schrödinger à l'aide de la
        relation de récurrence (équation (11))
    - Comparaison du nombre de nœuds avec le nombre quantique n
        - Si le nombre de nœuds est supérieur à n, on itère en affectant à }\mp@subsup{\varepsilon}{\mathrm{ max }}{}\mathrm{ la valeur }
        - Sinon on itère en affectant à }\mp@subsup{\varepsilon}{\mathrm{ min }}{}\mathrm{ la valeur }
Algorithme 1 - Résolution de l'équation de Schrödinger par une méthode dichotomique

Codage de l'algorithme

Note :
  • les codes demandés devront être réalisés dans le langage Python;
  • la bibliothèque numpy est supposée chargée et devra être utilisée pour représenter les tableaux unidimensionnels également appelés vecteurs;
  • une annexe présentant les fonctions usuelles de la bibliothèque numpy est disponible à la page 12;
  • les commentaires suffisant à la compréhension du programme devront être apportés et des noms de variables explicites devront être utilisés lorsque ceux-ci ne sont pas imposés.
L'intégration numérique de l'équation (6) se fait pour des valeurs de l'abscisse réduite comprises entre et . On note imax le nombre de valeurs des abscisses comprises entre et et le pas d'intégration . On souhaite diviser le segment en 100 intervalles de même longueur.
Q19. Donner la valeur numérique de imax. Donner le code permettant de calculer le pas en fonction de xmin, xmax et imax.
Q20. Donner le code permettant de calculer le vecteur xmesh qui contient les valeurs des abscisses réduites . Donner le code du calcul du vecteur vpot qui contient les valeurs du potentiel pour chaque abscisse réduite .
L'intégration numérique de l'équation de Schrödinger se fait en utilisant la relation de récurrence (11).
L'initialisation des 2 premiers termes de la série, et dépend de la parité de la fonction d'onde :
  • si est pair, on choisit et ;
  • si est impair, on choisit et .
Q21. En exploitant l'équation (11) et les propriétés de parité déduites de la question Q17, démontrer que dans le cas pair, .
On appelle nodes la variable, que l'on suppose définie, correspondant au nombre quantique , qui est aussi le nombre de nœuds de la fonction d'onde. On définit enfin , notée emin, à la valeur 0 et , notée emax, à la valeur maximale du vecteur vpot.
Q22. On note e la variable correspondant à l'énergie réduite . Écrire le code de la fonction calcul_f(e) qui calcule les valeurs de la fonction définie à la question Q15 pour chacun des contenu dans le vecteur xmesh et renvoie le vecteur f correspondant.
On souhaite maintenant développer une fonction calcul_y_noeuds(nodes, ) qui renvoie y (le vecteur contenant les valeurs de la fonction d'onde) et ncross (le nombre de nœuds). Sa structure est fournie dans le listing 1 qui est incomplet et dont le remplissage fait l'objet des questions suivantes.
def calcul_y_noeuds(nodes, f):
    "Calcul des valeurs de la fonction d'onde et du nombre de nœuds"
    # Calcul des valeurs initiales y0 et y1
    # Initialisation de la variable y
    y =
    # Nombre pair de nœuds
    if
        y[0]
        y[1] =
    # Nombre impair de nœuds
    else:
        y[0] =
        y[1] =
    # Intégration et comptage du nombre de nœuds
    # Initialisation de la valeur de ncross
    ncross =
    # Boucle de calcul des valeurs de y et du nombre de nœuds
    for i in range(___________):
        # Calcul la valeur de y[i]
        y[i] =
        # Calcul du nombre de nœuds
        ------------
    # Arguments de sortie de la fonction calcul_y_noeuds
    return
Listing 1 - Code à compléter de la fonction calcul_y_noeuds(nodes, £)
Q23. On souhaite que le comptage du nombre de nœuds, ncross, soit fait dans la boucle de calcul des valeurs de la fonction d'onde y (lignes 20 à 25 du listing 1). Donner une méthode simple permettant de réaliser le comptage (le code n'est pas demandé dans cette question).
Q24. Recopier et compléter le code de la fonction calcul_y_noeuds(nodes, ) fourni (voir listing 1). Les informations manquantes et attendues concernent:
  • l'initialisation de la variable y comme un vecteur nul de taille imax;
  • le test de la parité de la variable nodes;
  • le calcul des valeurs initiales et ;
  • l'initialisation de la variable ncross;
  • les instructions de début et de fin de la boucle de calcul des valeurs de et du nombre de nœuds;
  • le calcul des valeurs y[i];
  • le calcul du nombre de nœuds;
  • les arguments de sortie de la fonction calcul_y_noeuds.
Pour obtenir une valeur de suffisamment précise, on répète l'appel aux fonctions calcul_f(e) et calcul_y_noeuds(nodes, ) dans une boucle while avec une condition d'arrêt portant sur la différence qui doit être inférieure à une valeur suffisamment petite (on prendra dans le code) pour que l'on sorte de la boucle.
Q25. On suppose que la valeur de ncross a été calculée dans les étapes précédentes du code. Donner l'algorithme (le code est demandé à la question suivante) permettant de calculer la valeur de , notée e, pour l'itération suivante.
Q26. En utilisant l'algorithme 1, donner le code correspondant à la boucle permettant d'obtenir la valeur de par dichotomie. Elle doit faire intervenir les deux fonctions calcul_f(e) et calcul_y_noeuds(nodes, f).
La résolution numérique de l'équation de Schrödinger stationnaire pour l'oscillateur harmonique donne les valeurs suivantes pour les niveaux d'énergie (tableau 1) :
Niveau Énergie
0 0,5
1 1,5
2 2,5
3 3,5
4 4,5
5 5,5
Tableau 1 - Évolution de l'énergie en fonction de
Q27. À partir des données du tableau 1, proposer une expression de en fonction de vérifiée pour tout compris entre 0 et 5 .
Le calcul de l'entropie à partir des énergies déterminées précédemment ne sera pas abordé ici. La contribution que l'on obtient à la température de est égale à .

II. 3 - Comparaison des différents traitements de la rotation interne du groupe méthyle

Le tableau 2 rassemble les valeurs de la contribution de la rotation du groupe méthyle à l'entropie de la molécule d'éthane (notée ) pour les différents modèles et pour plusieurs températures. Les modèles utilisés pour le calcul sont le modèle de la rotation libre, celui de l'oscillateur harmonique et celui de la rotation empêchée qui correspond à la résolution de l'équation de Schrödinger avec le potentiel de la partie I.
Température 100 K 500 K 1000 K
Modèle de la rotation libre 7,5 12,0 14,2 17,1
Modèle de l'oscillateur harmonique 0,7 6,1 10,0 15,6
Modèle de la rotation empêchée 0,7 6,8 11,2 16,1
Tableau 2 - Valeurs de la contribution de la rotation du groupe méthyle à l'entropie de la molécule d'éthane ( en )
Q28. Commenter l'évolution globale avec la température de la contribution de la rotation du groupe méthyle à l'entropie de la molécule d'éthane. Justifier de manière qualitative la tendance observée.
Q29. En admettant que le modèle de la rotation empêchée fournit la meilleure estimation de la valeur de à toute température, préciser l'utilisation possible des deux autres modèles en fonction de la température.
Q30. Justifier qualitativement l'ordre des valeurs de la contribution de la rotation du groupe méthyle à l'entropie de la molécule d'éthane obtenue pour les trois modèles,
êé

ANNEXE

Bibliothèque numpy de Python

La bibliothèque numpy est importée de la façon suivante :
>>> import numpy as np
La création d'un tableau numpy à une dimension, appelé tab, possédant éléments tous initialisés à 0 , est réalisée ainsi :
>>> n = 4
>>> tab = np.zeros(n)
>>> print(tab)
[0.0.0.0.]
L'accès à un élément du tableau tab, en lecture ou en écriture, se fait à l'aide de la commande tab[i], la numérotation des indices démarrant à partir de 0 :
>>> tab = np.zeros(4)
>>> print(tab)
[0. 0. 0. 0.]
>>> tab[1] = 2
>>> print(tab)
[0. 2. 0. 0.]
La création d'un tableau numpy à une dimension, appelé tab, possédant éléments uniformément répartis entre deux valeurs debut et fin, se fait avec :
>>> debut, fin = 0, 10
>>> n = 5
>>> tab = np.linspace(debut, fin, n)
>>> print(tab)
[0. 2.5 5. 7.5 10.]

FIN

CCINP Modélisation TPC 2020 - Version Web LaTeX | WikiPrépa | WikiPrépa