Version interactive avec LaTeX compilé
Epreuve de Physique C - Chimie
Durée 2 h
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.
L'usage de calculatrices est autorisé.
A RENDRE AVEC LA COPIE : 1 DOCUMENT RÉPONSE
AVERTISSEMENT
La présentation, la lisibilité, l'orthographe, la qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l'appréciation des copies. En particulier, les résultats non encadrés et non justifiés ne seront pas pris en compte.
Chimie de quelques composés du soufre
Le soufre est un élément engagé dans de multiples minerais métalliques (blende, pyrite...). Le traitement de ces minerais produit donc, entre autres composés secondaires, l'une ou l'autre des structures moléculaires existantes contenant l'élément soufre. On récupère ce produit secondaire qu'on introduit dans la chaîne du soufre.
Par ailleurs, le soufre est présent dans les gisements méthaniers, dans les gisements pétroliers, sous forme de sulfure d'hydrogène
Ce problème a pour objectif de souligner plusieurs aspects de la chimie du soufre et de ses dérivés.
Par ailleurs, le soufre est présent dans les gisements méthaniers, dans les gisements pétroliers, sous forme de sulfure d'hydrogène
Ce problème a pour objectif de souligner plusieurs aspects de la chimie du soufre et de ses dérivés.
I. Premier exemple de chaîne de transformation : le minerai de zinc
I.1. Cristallographie de la Blende, minerai de ZnS
Le sulfure de zinc cristallise, dans la blende, selon un système cubique à faces centrées d'ions
I.1.1. Dessiner la maille correspondante. Indiquer le nombre d'ions de chaque espèce par maille.
I.1.2. Déterminer l'indice de coordination (coordinence, ou nombre des plus proches voisins de signe contraire) de chaque ion, ainsi que la distance correspondante
I.1.3. Le paramètre de maille vaut :
I.1.4. Montrer que le rapport des rayons ioniques vérifie l'inégalité
L1.5. Calculer la taille des sites tétraédriques de ce système. Quelle conclusion peut-on en tirer ?
Masses molaires :
I.1.1. Dessiner la maille correspondante. Indiquer le nombre d'ions de chaque espèce par maille.
I.1.2. Déterminer l'indice de coordination (coordinence, ou nombre des plus proches voisins de signe contraire) de chaque ion, ainsi que la distance correspondante
I.1.3. Le paramètre de maille vaut :
I.1.4. Montrer que le rapport des rayons ioniques vérifie l'inégalité
L1.5. Calculer la taille des sites tétraédriques de ce système. Quelle conclusion peut-on en tirer ?
Masses molaires :
I.2. Transformation du minerai
I.2.1. Grillage de ZnS
Le sulfure de zinc constitue le premier maillon de la chaîne de production du zinc métallique. La première étape de l'obtention du zinc consiste à griller ZnS dans le dioxygène.
I.2.1.1. Sachant qu'il se forme de l'oxyde de zinc(II) (appelé calcine) et du dioxyde de soufre gazeux, écrire l'équation de la réaction, pour une mole de ZnS .
I.2.1.2. Calculer l'enthalpie standard de la réaction ci-dessus à
I.2.1.3. A P constante, cette transformation est-elle favorisée à température faible ou élevée ? Justifier votre réponse.
I.2.1.1. Sachant qu'il se forme de l'oxyde de zinc(II) (appelé calcine) et du dioxyde de soufre gazeux, écrire l'équation de la réaction, pour une mole de ZnS .
I.2.1.2. Calculer l'enthalpie standard de la réaction ci-dessus à
I.2.1.3. A P constante, cette transformation est-elle favorisée à température faible ou élevée ? Justifier votre réponse.
Données thermodynamiques (298 K) :
| Composé |
|
|
|
|
|
|
-297 | 0 | -348 | -206 |
I.2.2 Lixiviation de l'oxyde de zinc
La lixiviation consiste ici à attaquer le minerai par une solution aqueuse acide ou alcaline L'oxyde de zinc préparé précédemment est impur. Il contient de nombreuses impuretés métalliques, dont
I.2.2.1. A l'aide des diagrammes
I.2.2.1. A l'aide des diagrammes
On réalise alors la seconde lixiviation. Le pH du milieu est modifié par ajout de calcine préparée antérieurement. C'est un oxyde "basique".
I.2.2.2. Indiquer pourquoi l'ajout de calcine modifie le pH du milieu : écrire l'équation de sa réaction avec l'eau.
I.2.2.3. Pourquoi n'ajoute-t-on pas une base plus commune, comme la soude, directement dans le milieu?
I.2.2.4. On introduit également, à ce niveau de la transformation, du dioxygène dans le milieu réactionnel.
Après avoir complété le diagramme
I.2.2.2. Indiquer pourquoi l'ajout de calcine modifie le pH du milieu : écrire l'équation de sa réaction avec l'eau.
I.2.2.3. Pourquoi n'ajoute-t-on pas une base plus commune, comme la soude, directement dans le milieu?
I.2.2.4. On introduit également, à ce niveau de la transformation, du dioxygène dans le milieu réactionnel.
Après avoir complété le diagramme
Données thermodynamiques utilisées pour le tracé et l'étude du diagramme
Finalement, on obtient une solution aqueuse acide de sulfate de zinc, impure, car elle contient différents cations métalliques qui n'ont pu être éliminés par les opérations précédentes.
Finalement, on obtient une solution aqueuse acide de sulfate de zinc, impure, car elle contient différents cations métalliques qui n'ont pu être éliminés par les opérations précédentes.
I.2.3. Cémentation de la solution sulfurique
La cémentation consiste à ajouter une fine poudre de zinc à la solution précédente.
Montrez qu'à l'issue de cette opération on obtient une solution aqueuse débarrassée de la plupart des cations autres que
Montrez qu'à l'issue de cette opération on obtient une solution aqueuse débarrassée de la plupart des cations autres que
Données thermodynamiques
Afin d'obtenir le zinc, cette solution doit être électrolysée : c'est une étude qui dépasse le cadre strictement thermodynamique développé ici.
II. Second exemple de chaîne de transformation : le soufre
II.1. Oxydation du sulfure d'hydrogène
Données numériques
Fonction amine :
Le dioxyde de soufre est obtenu, de manière principale, par désulfuration du gaz naturel (méthane), du pétrole et du charbon.
On fait passer un courant de méthane impur, contenant
II.1.1. Expliquer pourquoi cette solution permet de récupérer la très grande majorité de
I.1.2. Ecrire l'équation de la réaction
II.1.3. Cette première dissolution a lieu, dans l'industrie, à
II.1.4. Après avoir isolé la solution obtenue, on régénère
Justifier brièvement ces conditions réactionnelles.
On fait passer un courant de méthane impur, contenant
II.1.1. Expliquer pourquoi cette solution permet de récupérer la très grande majorité de
I.1.2. Ecrire l'équation de la réaction
II.1.3. Cette première dissolution a lieu, dans l'industrie, à
II.1.4. Après avoir isolé la solution obtenue, on régénère
Justifier brièvement ces conditions réactionnelles.
L'oxydation de
On opère à la température de
On fait alors réagir le dioxyde de soufre formé sur
On fait alors réagir le dioxyde de soufre formé sur
Données thermodynamiques (298 K)
| Composé |
|
|
|
|
|
|
|
|
-297 | 0 | -242 |
|
0 | 1,7 |
|
|
248,6 | 205 | 188,8 | 205,7 | 31,8 | 36,3 |
II.1.5. Calculer la valeur de
II.1.6. Cette dernière réaction est une réaction de rétro-dismutation : expliquer ce terme, en indiquant à quel élément il s'applique ici.
II.1.7. Après avoir rappelé l'approximation d'Ellingham, déterminer la température d'inversion
II.1.8. Le soufre obtenu est refroidi afin de l'obtenir sous forme solide : quel est l'intérêt de cette opération?
II.2. Oxydation du soufre en dioxyde de soufre
La réaction est la suivante :
On réalise la transformation à
II.2.1. Quel intérêt y a-t-il à utiliser du dioxygène en excès ?
II.2.2. La présence de diazote en quantité importante est-elle favorable à la transformation envisagée, dans ces conditions ?
II.2.1. Quel intérêt y a-t-il à utiliser du dioxygène en excès ?
II.2.2. La présence de diazote en quantité importante est-elle favorable à la transformation envisagée, dans ces conditions ?
II.3. Oxydation de
Données thermodynamiques à
| Composé |
|
|
|
|
|
|
-297 | 0 | -396 | 0 |
|
|
39,9 | 29,4 | 50,7 | 29,1 |
Il s'agit d'une étape importante de synthèse industrielle de l'acide sulfurique. On utilise, dans l'industrie, le dioxygène de l'air. Cette réaction (en phase gaz) se fait vers
II.3.1. Calculer, à
II.3.2. Calculer, à
II.3.3. On part de 10 moles de
II.3.2. Calculer, à
II.3.3. On part de 10 moles de
A
II.3.4. On suppose que la réaction se déroule dans un réacteur monobare adiabatique.
II.3.4. On suppose que la réaction se déroule dans un réacteur monobare adiabatique.
- Expliquer comment calculer la température finale du système,
. - Effectuer ce calcul.
III. L'élément soufre en solution aqueuse : le degré (-II)
L'élément soufre existe en solution aqueuse, notamment au degré d'oxydation (- II) : il est présent dans l'acide sulfhydrique, ou l'ion sulfure. Données :
III.1. Relation entre structure moléculaire et propriétés physiques macroscopiques
III.1.1. Donner les représentations de Lewis des molécules d'eau et de sulfure d'hydrogène ; indiquer leur notation dans le système VSEPR ; en déduire leur géométrie.
III.1.2. A l'aide vos connaissances de cours, justifier les températures de changement d'état observées (sous
III.1.3. Comparer la solubilité du gaz
On rappelle que la solubilité d'un composé est le nombre de moles de ce composé que l'on peut dissoudre dans un litre d'eau.
Données : saturation de l'eau en
III.1.2. A l'aide vos connaissances de cours, justifier les températures de changement d'état observées (sous
III.1.3. Comparer la solubilité du gaz
On rappelle que la solubilité d'un composé est le nombre de moles de ce composé que l'on peut dissoudre dans un litre d'eau.
Données : saturation de l'eau en
| Molécules |
|
|
Solubilité
|
|
|
0 | 100 | -- |
|
|
-86 | -61 |
|
|
|
|
||
| HCl | 20 | ||
|
|
50 |
III.2. Solubilité de
L'équilibre physico-chimique qui régit la solubilisation de
III.2.1. A l'équilibre, il est décrit par la relation
- Retrouver la valeur de la solubilité
de dans l'eau, à . - Comment la pression en
influence-t-elle cet équilibre? Justifier votre réponse.
III.2.2. Déterminer le pH et la composition d'une solution aqueuse d'acide sulfhydrique àmol. .
III.2.3. Pour une solution saturée en, sous , exprimer la concentration en ion sulfure dissous, en fonction de et ; en déduire l'expression de en fonction du pH .
III.3. Précipitation de sulfures métalliques
Les cations métalliques forment, avec les ions sulfure, des composés très peu solubles. Ce fait expérimental permet donc de détecter leur présence en solution. Ce test (dit «des sulfures») a été longuement utilisé en analyse minérale qualitative.
On considère une solution aqueuse contenant du cuivre, du fer et du nickel, sous forme d'ions
On fait barboter, dans la solution aqueuse contenant ces ions, un courant de sulfure d'hydrogène
On cherche à faire précipiter séparément les sulfures de fer, de nickel et de cuivre, sachant que les concentrations initiales des cations métalliques sont dans les rapports :
III.3.1. Exprimer la constante de solubilité d'un sulfure métallique
En déduire l'expression du
III.3.2. Montrer qu'il est possible de faire précipiter (et de récupérer) séparément chacun des sulfures, en modifiant le pH des solutions. On calculera les bornes des intervalles de pH dans lesquels chacun des sulfures précipite. Indiquer, sur un axe, les valeurs de ces intervalles de pH .
On considère une solution aqueuse contenant du cuivre, du fer et du nickel, sous forme d'ions
On fait barboter, dans la solution aqueuse contenant ces ions, un courant de sulfure d'hydrogène
On cherche à faire précipiter séparément les sulfures de fer, de nickel et de cuivre, sachant que les concentrations initiales des cations métalliques sont dans les rapports :
III.3.1. Exprimer la constante de solubilité d'un sulfure métallique
En déduire l'expression du
III.3.2. Montrer qu'il est possible de faire précipiter (et de récupérer) séparément chacun des sulfures, en modifiant le pH des solutions. On calculera les bornes des intervalles de pH dans lesquels chacun des sulfures précipite. Indiquer, sur un axe, les valeurs de ces intervalles de pH .
Données thermodynamiques :
III.3.3. Comment peut-on fixer le pH d'une solution aqueuse? Justifier votre réponse, en l'illustrant sur un exemple concret.
III.3.3. Comment peut-on fixer le pH d'une solution aqueuse? Justifier votre réponse, en l'illustrant sur un exemple concret.
Annexe
Diagramme
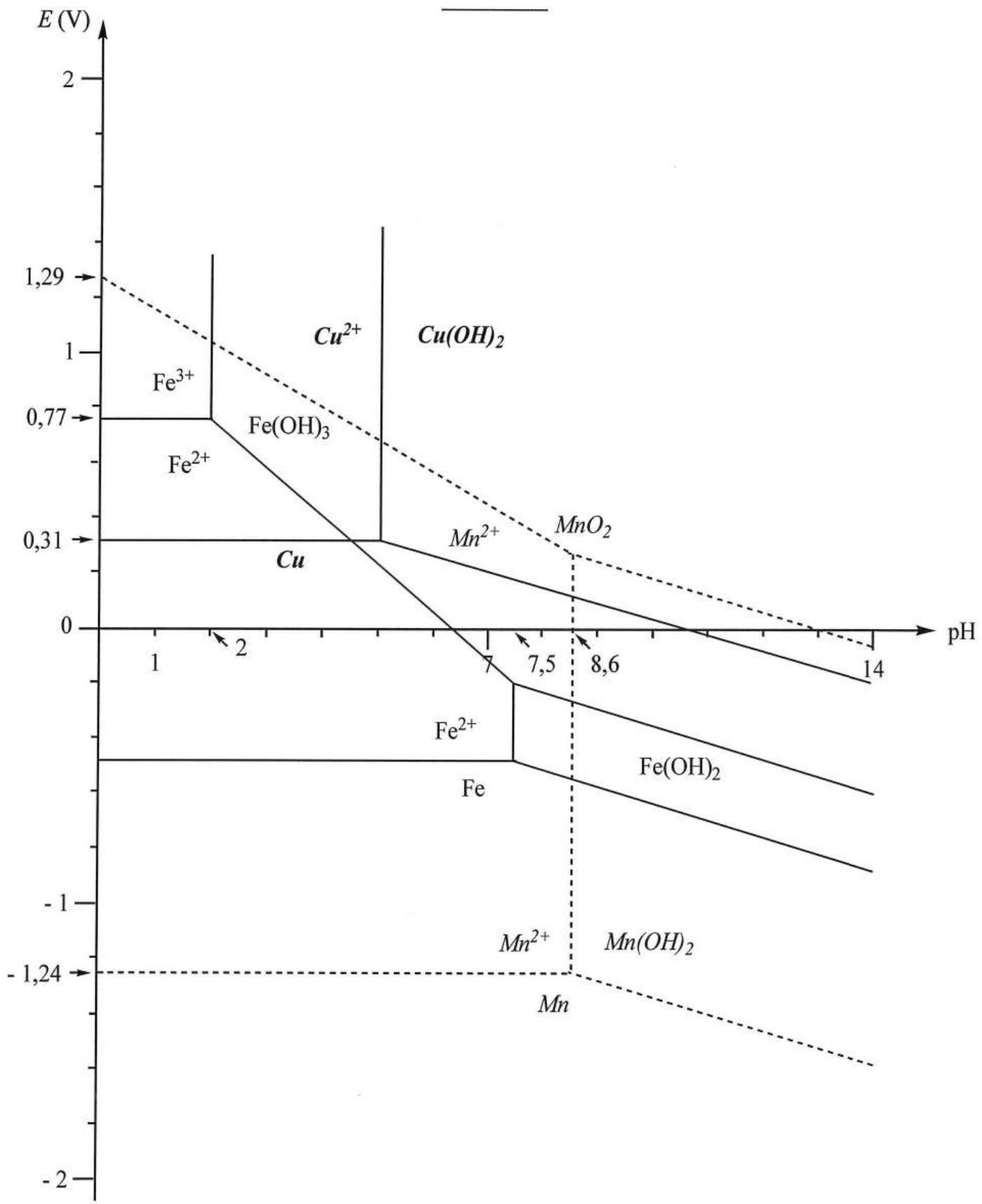
Fer et Manganèse :
Cuivre :
Cuivre :
Epreuve de Physique C - Thermodynamique
Si , au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.
L'usage de calculatrices est autorisé.
A RENDRE AVEC LA COPIE : 1 DOCUMENT RÉPONSE
AVERTISSEMENT
La présentation, la lisibilité, l'orthographe, la qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l'appréciation des copies. En particulier, les résultats non encadrés et non justifiés ne seront pas pris en compte.
On se propose d'étudier dans ce problème le fonctionnement d'une turbine à gaz (ou turbine à combustion). Elles fonctionnent habituellement selon un cycle ouvert selon le schéma de la Figure 1.
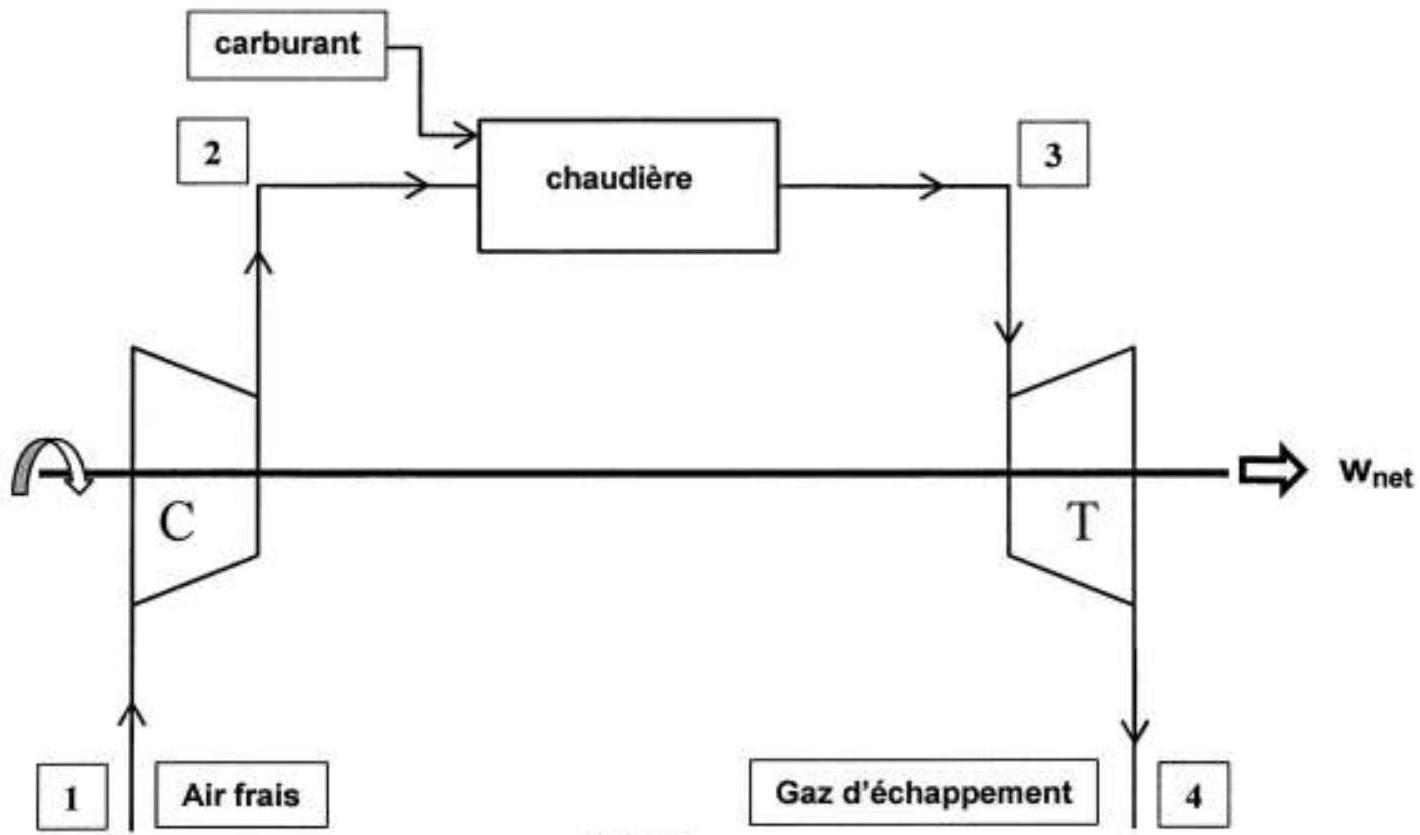
Figure 1
L'air frais pris à l'atmosphère est comprimé à haute pression dans le compresseur (C) puis il est admis dans la chambre de combustion (chaudière). Les gaz chauds résultants de la combustion se détendent alors dans la turbine (T) avant d'être évacués à l'atmosphère sous forme de gaz d'échappement.
Le compresseur et la turbine sont montés sur le même arbre permettant de récupérer un travail noté
Le compresseur et la turbine sont montés sur le même arbre permettant de récupérer un travail noté
I. PRELIMINAIRES
Considérons une machine thermodynamique ouverte telle que présentée sur la Figure 2. Le fluide s'écoule en régime permanent avec un débit massique noté D . Il entre dans la machine à une altitude
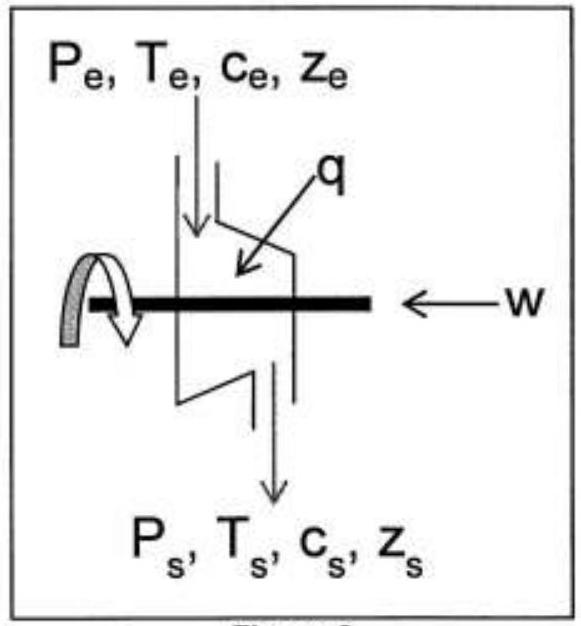
Figure 2
1- Montrer que le premier principe de la thermodynamique appliqué à un système que vous préciserez soigneusement, permet d'établir l'expression suivante :
avec :
- h enthalpie massique du fluide
- q transfert thermique massique reçu par le fluide de l'extérieur lorsqu'il est dans la machine
- w travail massique indiqué reçu par le fluide de l'extérieur lorsqu'il traverse la machine.
w et q étant pris comme des grandeurs algébriques.
2- Par la suite on sera amené à étudier un écoulement d'air supposé gaz parfait, non pesant et de variation d'énergie cinétique négligeable. On notera alorset les capacités thermiques
massiques à pression et volume constants. Elles seront considérées indépendantes de la température et de rapport :
En appliquant les hypothèses précédentes et à partir de l'expression démontrée dans la question 1, proposez une expression simplifiée faisant intervenir les températures d'entrée et de sortie du fluide.
3- On note R la constante molaire des gaz parfaits et M la masse molaire de l'air. Déterminer
4- Pour l'air on prend
II. MODELISATION IDEALE DU CYCLE : CYCLE DE JOULE
Le cycle ouvert présenté en Figure 1, peut être modélisé comme un cycle fermé. Ce cycle est présenté sur la Figure 3.
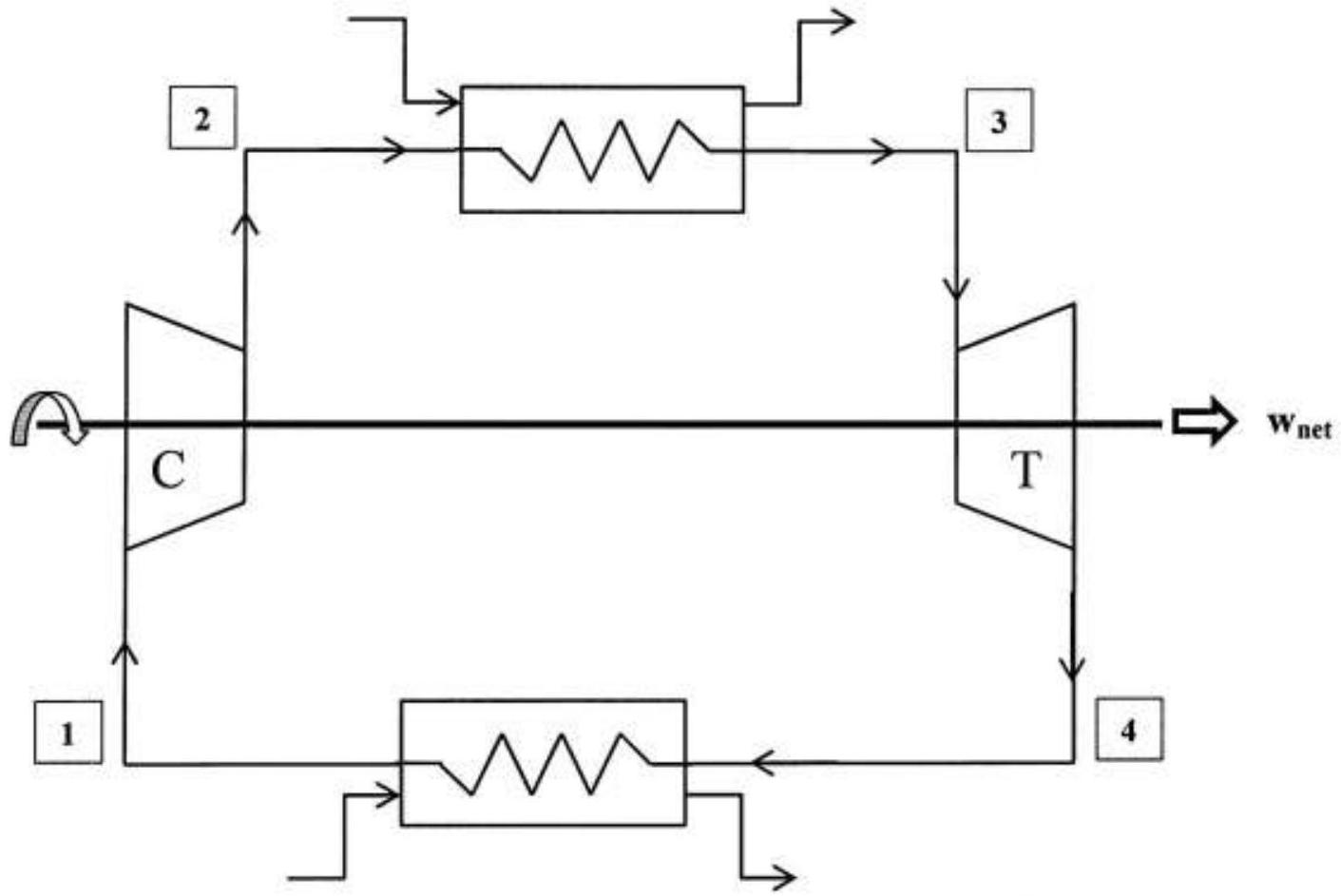
Figure 3
Les évolutions de compression et de détente restent inchangées. Le phénomène de combustion est remplacé par une évolution d'échange de chaleur à pression constante avec une source de chaleur externe. L'échappement des gaz brûlés et l'admission d'air frais est remplacé par une évolution d'échange de chaleur à pression constante avec le milieu extérieur.
L'air subi une succession de 4 évolutions réversibles au cours du cycle :
- au point 1 l'air entre dans le compresseur pour y subir une compression isentropique jusqu'au point 2.
- entre les points 2 et 3 l'air échange de la chaleur avec un fluide extérieur dans un échangeur de chaleur isobare modélisant la chaudière.
- au point 3 l'air entre dans la turbine pour y subir une détente isentropique jusqu'au point 4.
- entre les points 4 et 1 l'air échange de la chaleur avec l'atmosphère dans un échangeur de chaleur isobare. L'air du cycle est ainsi refroidi.
5- On note v le volume massique de l'air. Représenter dans le diagramme de Clapeyron (P,v) le cycle subi par l'air. On précisera les points
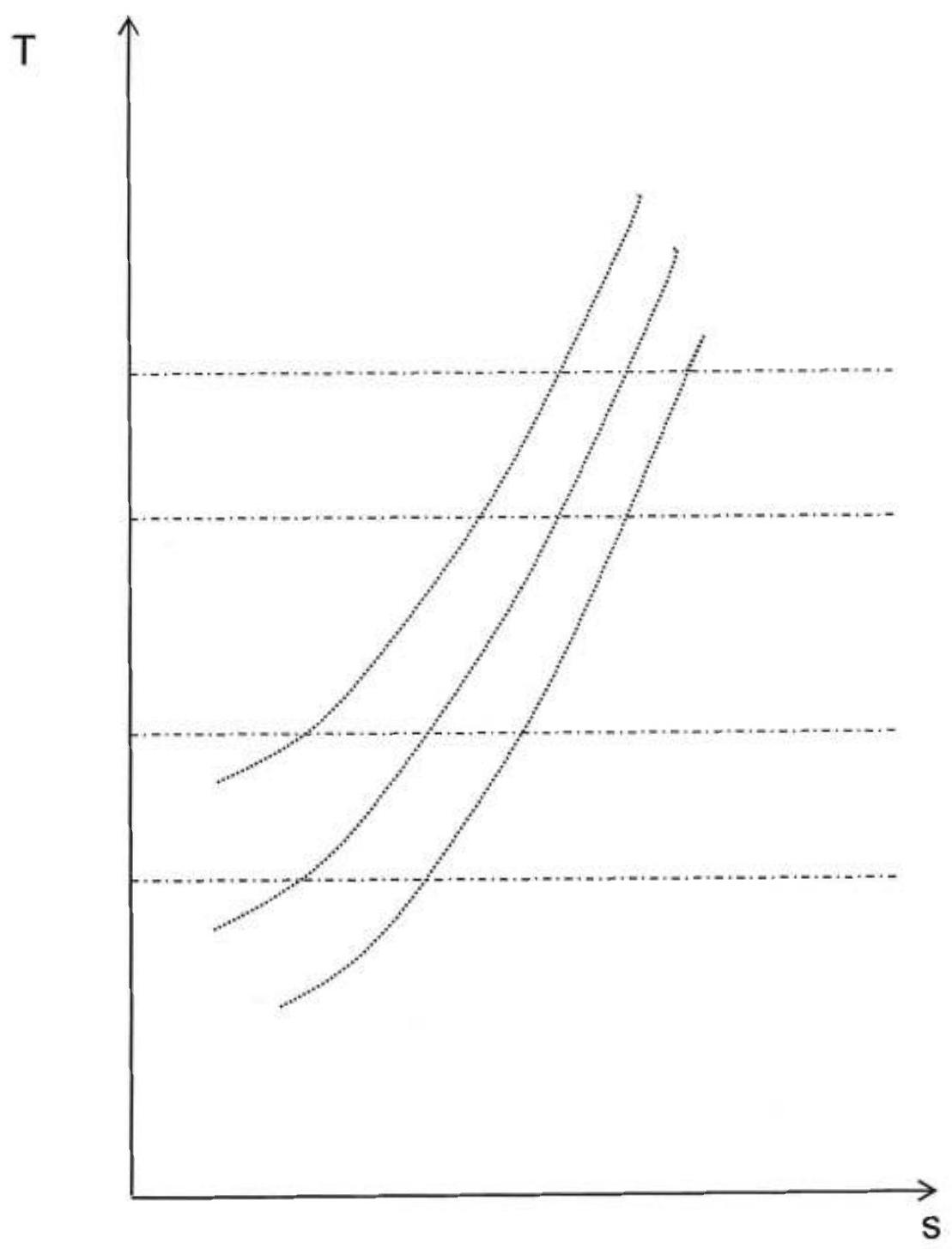
On donne le cycle dans le diagramme (
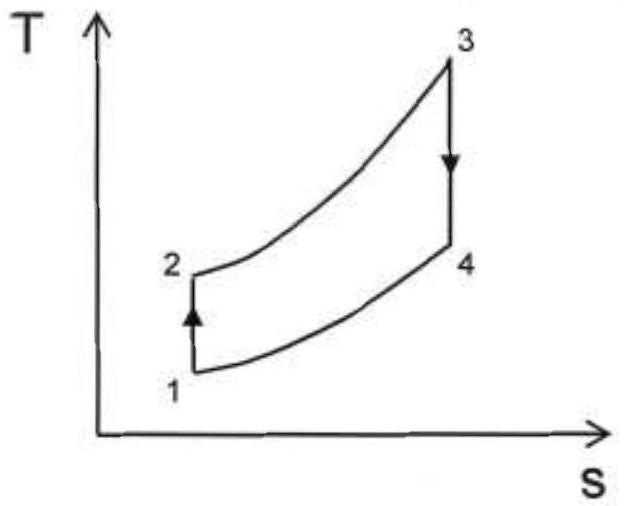
Figure 4
6- Exprimer l'entropie massique de l'air à la température
7- En déduire qu'une évolution isobare se représente comme une exponentielle conformément au cycle tracé dans le diagramme (
7- En déduire qu'une évolution isobare se représente comme une exponentielle conformément au cycle tracé dans le diagramme (
Détermination des grandeurs énergétiques
Par la suite on notera toute grandeur relative au point i du cycle,
8- Déterminer les transferts thermiques subis par l'air dans les deux échangeurs de chaleur que l'on notera respectivement
9- Déterminer le travail massique, noté
10-Déterminer le travail massique, noté
9- Déterminer le travail massique, noté
10-Déterminer le travail massique, noté
11-Exprimer
12- En déduire une expression de
12- En déduire une expression de
Expression du rendement et optimisation
13- Définir le rendement de l'installation.
14- Montrer que l'on peut le mettre sous la forme :
14- Montrer que l'on peut le mettre sous la forme :
15- On introduit le taux de compression défini par :
Montrer alors que l'on peut mettre le rendement sous la forme :
avec
16-D'après la question précédente, sur quelle grandeur peut-on influer pour augmenter le rendement ? Au cours d'une étude technico-commerciale du dispositif, quel autre élément faudra-t-il prendre en compte pour concevoir la turbine à gaz ?
Optimisation du travail récupéré sur l'arbre
On impose le fonctionnement de cette turbine à gaz à
17-Dans le diagramme de Clapeyron, que représente l'aire du cycle subi par le fluide? On justifiera avec soin la réponse.
18-Par le même type de raisonnement, en déduire ce que représente l'aire du cycle subi par le fluide en diagramme (
19- Pourquoi alors obtient-on par simple lecture de l'aire du cycle subi par le fluide en diagramme (
20-Les températures des points 1 et 3 du cycle étant fixées ainsi que la pression entre les points 4 et 1 du cycle, représenter le cycle de Joule (en diagramme (T,s)), dans les deux cas suivants :
a. Un rapport de compression tel que
b. Un rapport de compression tel que
17-Dans le diagramme de Clapeyron, que représente l'aire du cycle subi par le fluide? On justifiera avec soin la réponse.
18-Par le même type de raisonnement, en déduire ce que représente l'aire du cycle subi par le fluide en diagramme (
19- Pourquoi alors obtient-on par simple lecture de l'aire du cycle subi par le fluide en diagramme (
20-Les températures des points 1 et 3 du cycle étant fixées ainsi que la pression entre les points 4 et 1 du cycle, représenter le cycle de Joule (en diagramme (T,s)), dans les deux cas suivants :
a. Un rapport de compression tel que
b. Un rapport de compression tel que
21-En déduire que
22- Exprimer le travail net
23-Déterminer par le calcul la valeur de
24-En déduire la valeur maximale que
25- Calculer numériquement
22- Exprimer le travail net
23-Déterminer par le calcul la valeur de
24-En déduire la valeur maximale que
25- Calculer numériquement
III. MISE EN PLACE D'UNE COMPRESSION ETAGEE
La compression des gaz est une opération délicate et surtout très coûteuse. Pour répondre à ce problème, on est amené à procéder à une compression étagée comme proposé sur la partie droite de la Figure 5.
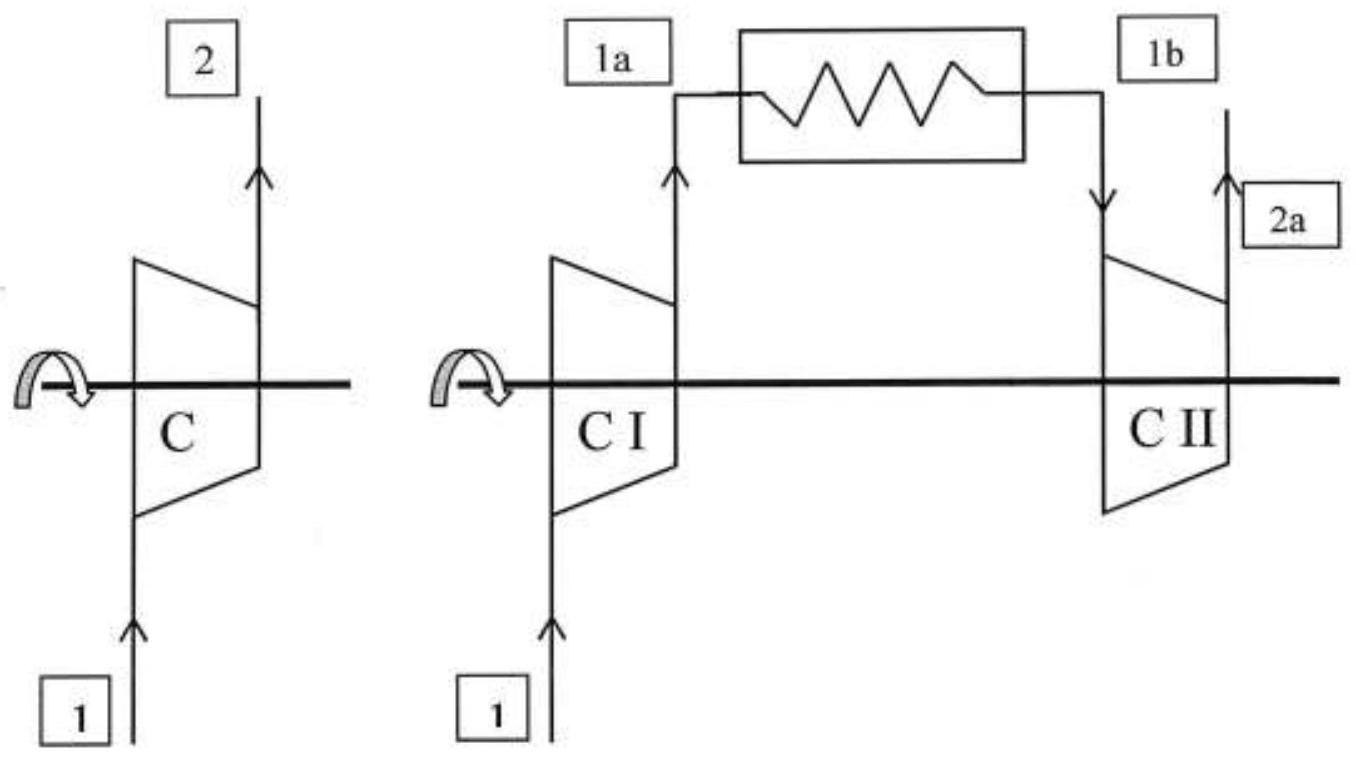
Figure 5 : Compression à un étage (à gauche) à deux étages (à droite)
Au point 1 , l'air est sous la pression
Compression à un étage :
Compression à un étage :
- Evolution
compression isentropique de à .
Compression à deux étages :
- Evolution
compression isentropique de à . - Evolution 1a
refroidissement isobare jusqu'à la température - Evolution 1b
: compression isentropique de à .
26-On donne en Figure 6, le tracé à partir d'un point 1 du diagramme de Clapeyron, deux évolutions : l'une isotherme, l'autre isentropique. Reprenez sur votre copie ce diagramme en identifiant le tracé de l'évolution isentropique et de l'évolution isotherme. On justifiera la réponse en démontrant une relation entre la pente d'une isotherme et la pente d'une isentropique.
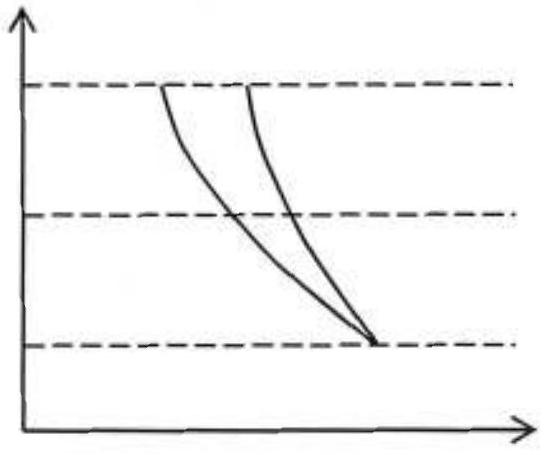
Figure 6
27- Toujours à partir de la Figure 6, tracer un nouveau diagramme de Clapeyron en y faisant figurer la courbe représentative de l'évolution de
28-En déduire par un raisonnement graphique, l'intérêt d'une compression à deux étages par rapport à la compression à un étage.
29-Dans un diagramme entropique (
28-En déduire par un raisonnement graphique, l'intérêt d'une compression à deux étages par rapport à la compression à un étage.
29-Dans un diagramme entropique (
On pourrait alors montrer que, pour obtenir un travail minimal de compression, il faut choisir un rapport de pression entre chaque étage identique. A savoir ici:
IV. TURBINE A GAZ AVEC COMPRESSEUR ET TURBINE A DEUX ETAGES ET REGENERATEUR
Ce que l'on vient de montrer lors de la partie III, avec le compresseur est valable aussi pour la turbine. La Figure 7 représente le schéma de fonctionnement d'une turbine à gaz comprenant un compresseur à deux étages, une chambre de combustion, une turbine à deux étages puis un
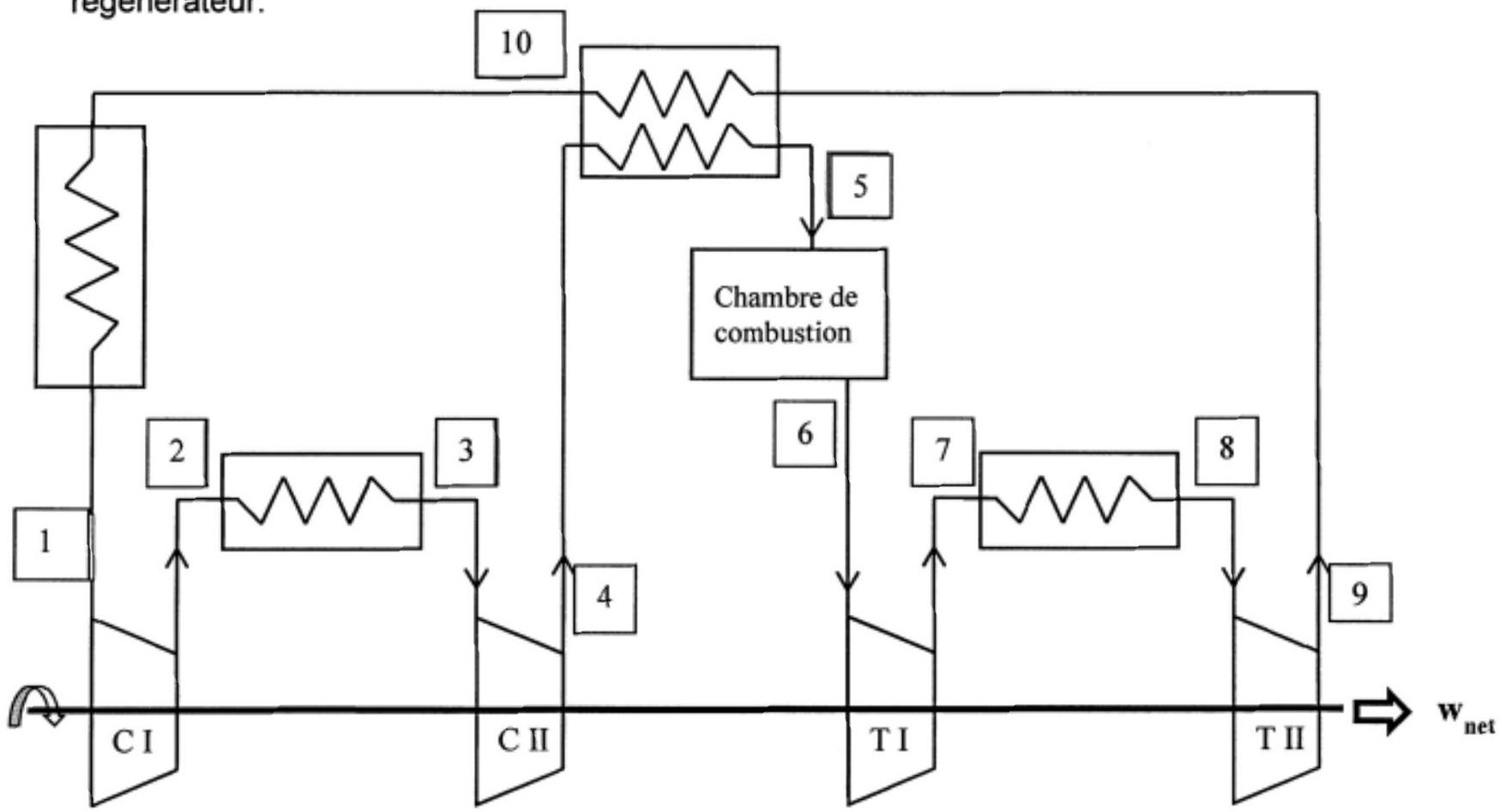
Figure 7
Les évolutions subies par l'air sont les suivantes:
Conformément à ce qui a été dit à la fin de la partie III, le rapport des pressions de chaque étage doit être le même. Ce résultat est aussi valable pour les étages de détente.
Conformément à ce qui a été dit à la fin de la partie III, le rapport des pressions de chaque étage doit être le même. Ce résultat est aussi valable pour les étages de détente.
Ce qui nous permet de poser :
30-Dans le diagramme (
30-Dans le diagramme (
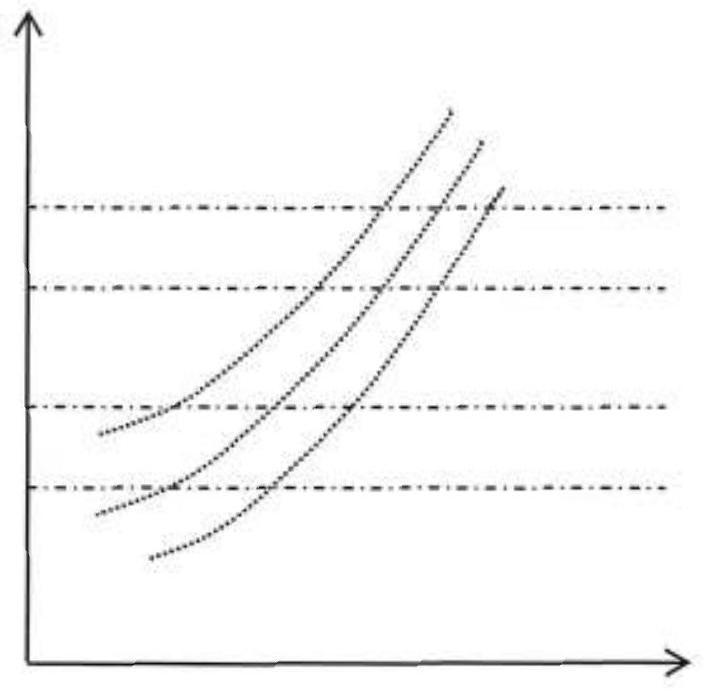
Figure 8
31- Où peut-on lire graphiquement par simple différence entre deux grandeurs
32- Exprimer alors le rendement de cette installation en fonction des différents transferts thermiques massiques et des travaux échangés au cours du cycle. En déduire une forme de ce rendement uniquement en fonction des températures
33- On désire augmenter le nombre d'étages de compression et de détente, tout en gardant un même rapport de compression (de détente) pour chaque étage de compression (de détente). Soit n étages de compression pour passer de
34-En déduire vers quelle valeur tend ce rapport si
On peut alors, dans le cas d'un nombre d'étage de compression et de détente infini, assimiler le cycle subi par l'air à un cycle composé de deux isobares
32- Exprimer alors le rendement de cette installation en fonction des différents transferts thermiques massiques et des travaux échangés au cours du cycle. En déduire une forme de ce rendement uniquement en fonction des températures
33- On désire augmenter le nombre d'étages de compression et de détente, tout en gardant un même rapport de compression (de détente) pour chaque étage de compression (de détente). Soit n étages de compression pour passer de
34-En déduire vers quelle valeur tend ce rapport si
On peut alors, dans le cas d'un nombre d'étage de compression et de détente infini, assimiler le cycle subi par l'air à un cycle composé de deux isobares
35- Tracer le cycle dans le diagramme (T,s).
36-Identifier sur ce schéma les évolutions correspondantes au fonctionnement du régénérateur, du réchauffement lors des détentes, et du refroidissement lors des compressions.
37-En appliquant le second principe de la thermodynamique, exprimer
38-De même, exprimer
39- En déduire l'expression du rendement en fonction des températures
40- Quelle remarque peut-on faire ? Dans la pratique, on se contente de 3 étages. Pourquoi ?
36-Identifier sur ce schéma les évolutions correspondantes au fonctionnement du régénérateur, du réchauffement lors des détentes, et du refroidissement lors des compressions.
37-En appliquant le second principe de la thermodynamique, exprimer
38-De même, exprimer
39- En déduire l'expression du rendement en fonction des températures
40- Quelle remarque peut-on faire ? Dans la pratique, on se contente de 3 étages. Pourquoi ?
DOCUMENT ANNEXE A RENDRE AVEC LA COPIE :
FIGURE 8