J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Banque PT Physique A PT 2024

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo banque-pt
🔗 Explorer
Banque
Banque PT
Année
2024
Filière
PT
Matière
Physique
Banque PT PTBanque PT 2024PT PhysiquePhysique 2024
2025_09_04_855efa9bb60aff0a9921g

Epreuve de Physique A

Durée 4 h
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.

L'usage de calculatrices est interdit.

AVERTISSEMENT

La présentation, la lisibilité, l'orthographe, la qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l'appréciation des copies. En particulier, les résultats non justifiés ne seront pas pris en compte. Les candidats sont invités à encadrer les résultats de leurs calculs.

CONSIGNES:

  • Composer lisiblement sur les copies avec un stylo à bille à encre foncée : bleue ou noire.
  • L'usage de stylo à friction, stylo plume, stylo feutre, liquide de correction et dérouleur de ruban correcteur est interdit.
  • Remplir sur chaque copie en MAJUSCULES toutes vos informations d'identification : nom, prénom, numéro inscription, date de naissance, le libellé du concours, le libellé de l'épreuve et la session.
  • Une feuille, dont l'entête n'a pas été intégralement renseigné, ne sera pas prise en compte.
  • Il est interdit aux candidats de signer leur composition ou d'y mettre un signe quelconque pouvant indiquer sa provenance
Ce sujet est composé de cinq parties indépendantes, qui portent sur le cycle de l'eau de pluie :
  • la première partie s'intéresse à la chute d'une gouttelette d'eau dans l'air (environ du barème) ;
  • la seconde partie s'intéresse à la formation d'un arc-en-ciel (environ du barème);
  • la troisième partie s'intéresse au fonctionnement d'un pluviomètre capacitif (environ du barème) ;
  • la quatrième partie s'intéresse au remplissage d'une nappe phréatique (environ du barème);
  • la cinquième partie s'intéresse à la production hydroélectrique d'un barrage (environ du barème).
On considère les valeurs numériques suivantes pour tout le sujet :
  • intensité de la pesanteur : ;
  • viscosité dynamique de l'air : ;
  • viscosité dynamique de l'eau : ;
  • masse volumique de l'air : ;
  • masse volumique de l'eau : .
Les résultats des applications numériques sont attendus avec seulement 1 chiffre significatif.

I. Chute d'une gouttelette d'eau dans l'air

Un nuage est constitué d'une grande quantité de gouttelettes d'eau en suspension dans l'air. Il se forme par condensation de la vapeur d'eau naturellement présente dans l'atmosphère lorsque les conditions météorologiques sont adéquates. Ces gouttelettes en suspension grossissent en se réunissant sous l'effet des courants atmosphériques jusqu'à atteindre une taille critique, au-delà de laquelle elles tombent sous forme de pluie. Dans cette partie, nous allons étudier la chute d'une gouttelette d'eau à l'aide de deux modélisations pour l'atmosphère: le cas d'une atmosphère sèche, puis le cas d'une atmosphère humide.

I.1. Cas d'une atmosphère sèche

Dans un premier temps, on étudie la chute d'une gouttelette d'eau sphérique de masse volumique et de rayon constant dans une atmosphère sèche, constituée d'air de masse volumique et de viscosité dynamique . On néglige tout phénomène d'évaporation au cours de cette chute. À l'instant , on suppose que la gouttelette quitte le nuage d'où elle provient, sans vitesse initiale. Elle est alors soumise à trois forces au cours de sa chute :
  • son poids ;
  • la poussée d'Archimède exercée par l'air ;
  • une force de frottement fluide exercée par l'air que l'on modélise sous la forme :
avec le vecteur vitesse de la gouttelette.
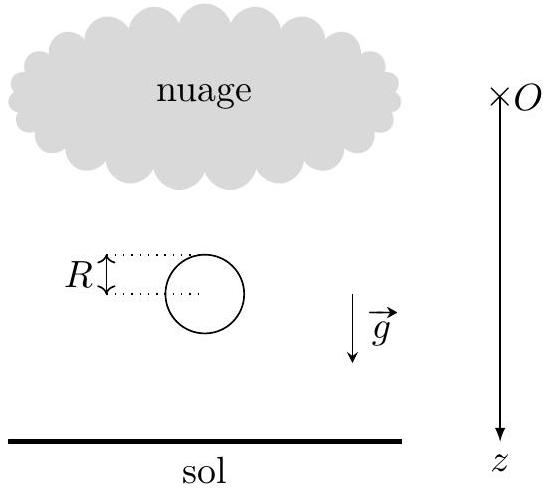
On définit l'axe ( ) vertical descendant, comme représenté sur la Figure 1.
Figure 1 : Chute d'une gouttelette d'eau de rayon constant dans une atmosphère sèche.
  1. Exprimer la norme de la poussée d'Archimède subie par la gouttelette en fonction des données de l'énoncé.
  2. Calculer numériquement le rapport, en norme, de la poussée d'Archimède sur le poids de la gouttelette, puis justifier qu'il est possible de négliger la poussée d'Archimède dans cette modélisation.
Dans la suite, on négligera ainsi toujours la poussée d'Archimède.
3. Établir l'équation différentielle vérifiée par la composante de la vitesse de la gouttelette projetée sur l'axe ( ) vertical descendant.
4. À partir de cette équation différentielle, définir un temps caractéristique en fonction de et , puis calculer sa valeur numérique.
5. En déduire l'expression de en fonction de et .
6. Calculer numériquement la vitesse limite vers laquelle tend la gouttelette au cours de sa chute.
L'expression de la force de frottement utilisée dans cette modélisation n'étant valable que dans le cas d'un écoulement laminaire, il est nécessaire de vérifier cette hypothèse.
7. Calculer numériquement le nombre de Reynolds de l'air qui s'écoule autour de la gouttelette au cours de sa chute, puis conclure sur la validité de cette hypothèse.

I.2. Cas d'une atmosphère humide

On étudie maintenant la chute d'une gouttelette d'eau sphérique de masse volumique dans une atmosphère humide, principalement constituée d'air de masse volumique et de viscosité dynamique . L'humidité du milieu fait croitre le rayon de la gouttelette au cours de sa chute, et on note sa masse. À l'instant , on suppose que la gouttelette quitte le nuage d'où elle provient, sans vitesse initiale et avec un rayon initial . En supposant que la poussée d'Archimède est toujours négligeable, la gouttelette est alors soumise à deux forces au cours de sa chute :
  • son poids ;
  • une force de frottement fluide exercée par l'air que l'on modélise sous la forme :
avec le vecteur vitesse de la gouttelette.
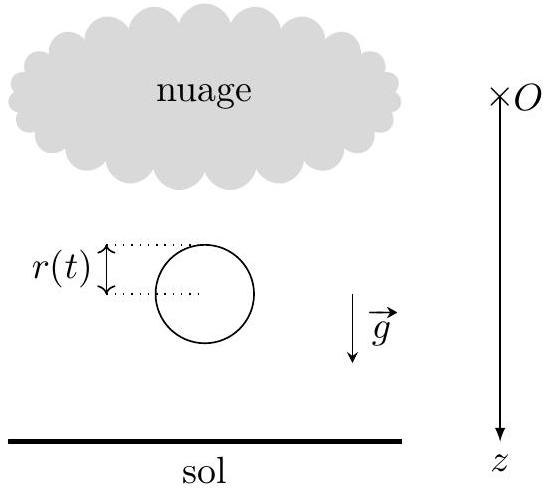
On définit l'axe ( ) vertical descendant, comme représenté sur la Figure 2.
Figure 2 : Chute d'une gouttelette d'eau de rayon variable dans une atmosphère humide.
  1. En supposant que l'augmentation du volume de la gouttelette au cours du temps est proportionnelle à sa surface, justifier que son rayon peut alors s'exprimer sous la forme :
avec une constante caractéristique de l'humidité du milieu, que l'on ne cherchera pas à exprimer.
9. Exprimer en fonction de et .
Dans le cas d'un système de masse variable , on peut montrer que la seconde loi de Newton reste valable dans un référentiel galiléen à condition de remplacer le terme , ce qui donne en développant: .
10. Montrer que l'équation différentielle vérifiée par la vitesse de la gouttelette projetée sur l'axe vertical descendant peut alors s'écrire sous la forme :
avec et des constantes que l'on exprimera en fonction de et .
Quelques instants après le début de sa chute, le rayon de la gouttelette devient suffisamment important pour que le terme de l'équation différentielle soit négligeable devant le terme .
11. En prenant en compte cette simplification, résoudre l'équation différentielle obtenue en résolvant d'abord l'équation sans second membre, puis en cherchant une solution particulière de l'équation complète sous la forme d'une fonction affine, afin d'en déduire l'expression de en fonction de et .
Lorsque le rayon de la gouttelette d'eau dépasse quelques millimètres, il n'est plus réaliste de considérer que la forme de celle-ci est encore sphérique. En effet, la trainée aérodynamique donne alors une forme de disque incurvé à la gouttelette d'eau, qu'il serait nécessaire de prendre en compte.
12. Grâce à votre culture scientifique, donner le nom de l'énergie par unité de surface qui est responsable de la forme sphérique des gouttelettes d'eau de petites tailles.

II. Formation d'un arc-en-ciel

Lorsque le beau temps revient juste après une averse, on observe parfois la formation d'un arc-enciel à l'horizon. Il s'agit d'un phénomène optique de dispersion de la lumière solaire, qui se réfracte et se réfléchit dans des gouttelettes d'eau en suspension dans l'air. La première théorie permettant d'expliquer ce phénomène a été établie par Descartes en 1637 à l'aide des lois de la réflexion et de la
réfraction. Il mit en évidence qu'un observateur situé au niveau du sol reçoit un faisceau de rayons émergents correspondant au maximum de l'angle de déviation des gouttelettes d'eau. Comme celui-ci dépend de la longueur d'onde des rayons lumineux, on peut ainsi observer la dispersion de la lumière solaire. Dans cette partie, nous allons mettre en évidence les principaux résultats de cette théorie.
On considère un rayon lumineux monochromatique issu du Soleil , qui arrive sur une gouttelette d'eau sphérique en suspension dans l'air sous un angle d'incidence , comme représenté sur la Figure 3. Après une première réfraction, une réflexion et une seconde réfraction, le rayon émerge de la gouttelette sous un angle de réfraction . Il se dirige alors vers un observateur situé au niveau du sol. On suppose que l'air est un milieu d'indice optique égal à 1 , et on note l'indice optique de l'eau.
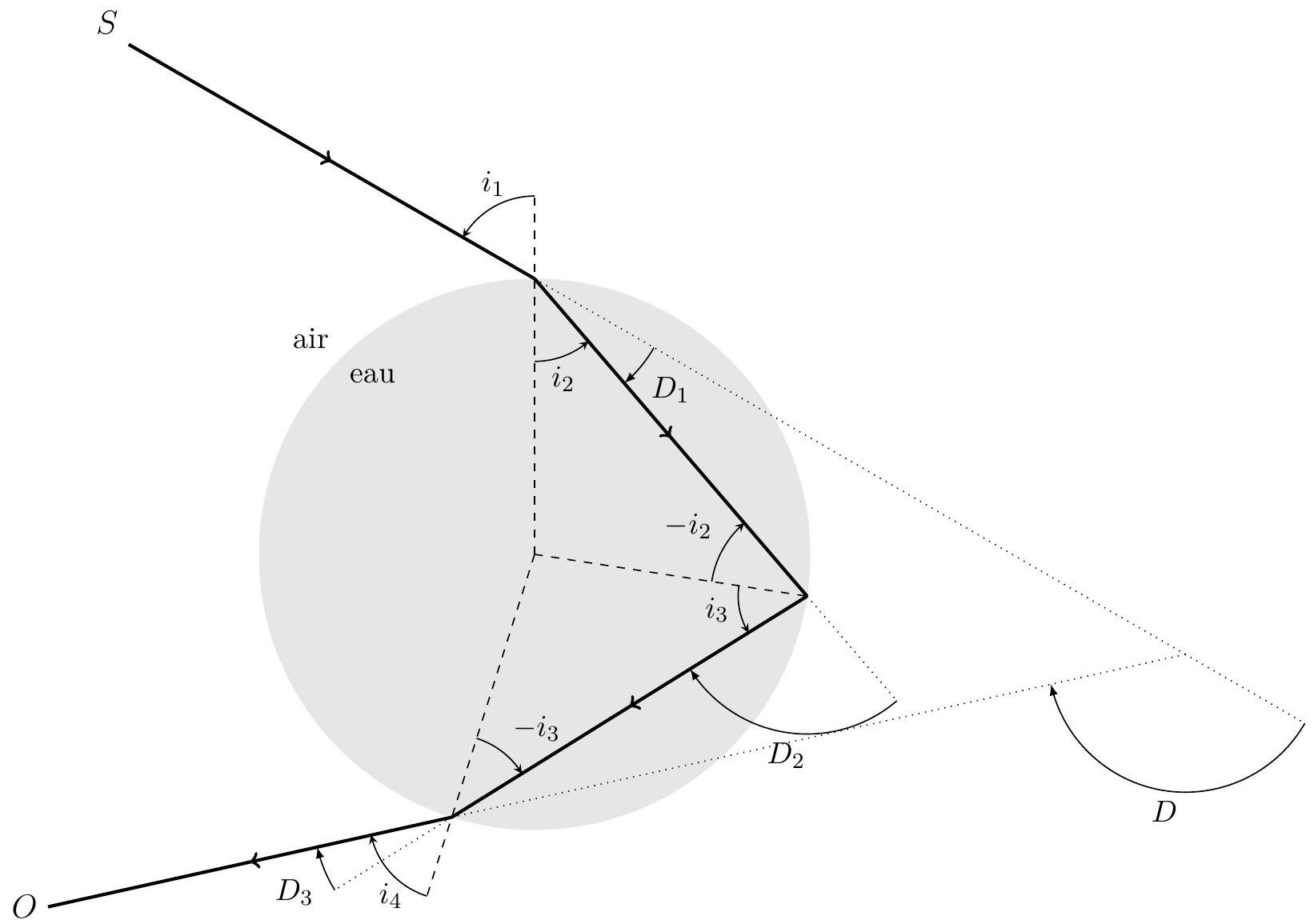
Figure 3 : Trajet d'un rayon lumineux dans une gouttelette d'eau sphérique en suspension dans l'air.
L'orientation des différents angles à chaque interface est définie sur la Figure 3, et on définit positivement les angles orientés dans le sens trigonométrique.
13. Exprimer les angles de déviation et à chaque interface en fonction de et (en tenant compte de l'orientation de ces angles).
14. À l'aide des lois de Snell-Descartes, exprimer les angles et en fonction de et .
15. En déduire que l'angle de déviation totale peut s'exprimer :
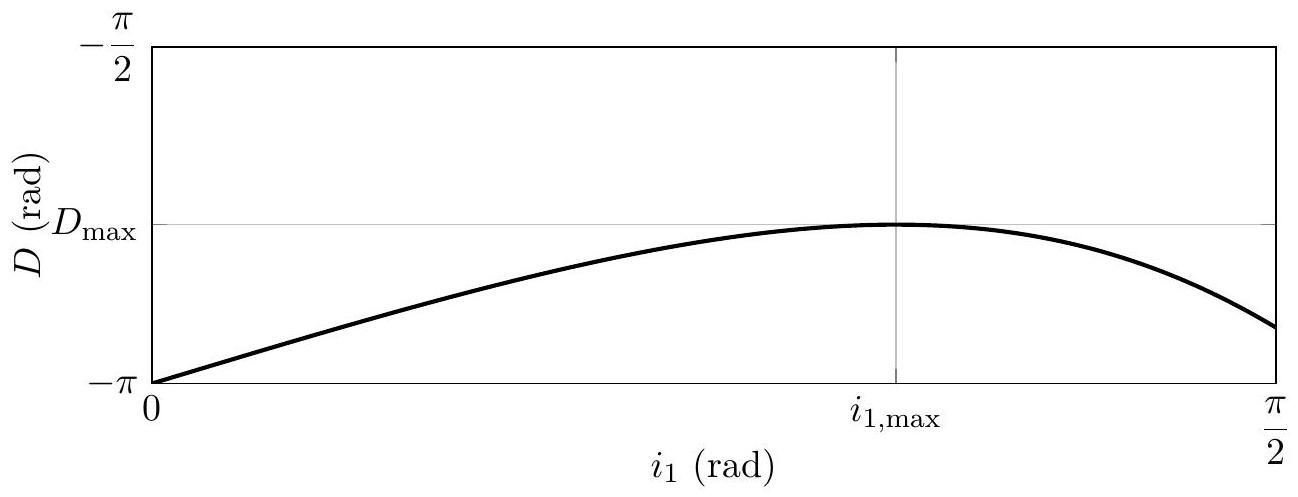
On représente l'évolution de en fonction de sur la Figure 4, en prenant pour l'indice optique de l'eau. L'angle de déviation présente un maximum pour un certain angle d'incidence qui correspond au faisceau de rayons émergents reçu par l'observateur.
Figure 4 : Évolution de l'angle de déviation en fonction de l'angle d'incidence .
On rappelle que la dérivée de la fonction trigonométrique s'exprime :
  1. Montrer que l'angle d'incidence vérifie l'équation suivante :
  1. En déduire l'expression du maximum en fonction de .
On représente l'évolution de en fonction de sur la Figure 5, pour .
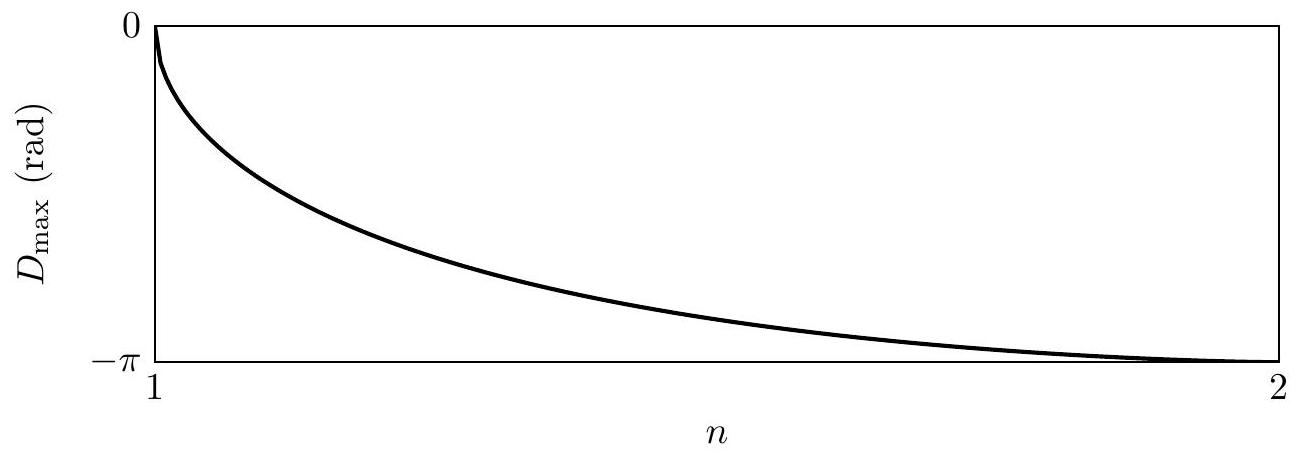
Figure 5 : Évolution du maximum en fonction de l'indice optique .
L'eau étant un milieu dispersif, son indice optique dépend de la longueur d'onde du rayon lumineux considéré. En 1836, Cauchy établit que l'indice optique d'un tel milieu peut s'exprimer sous la forme :
avec et des constantes positives caractéristiques du milieu.
18. Comment évolue le maximum lorsque la longueur d'onde augmente? Justifier votre raisonnement.
19. Rappeler l'intervalle de longueur d'onde constituant le spectre visible.
20. Lorsque l'observateur situé au niveau du sol regarde l'arc-en-ciel, aperçoit-t-il l'anneau rouge situé au-dessus ou en-dessous de l'anneau violet? Justifier votre raisonnement.
Lorsque les conditions d'observation sont excellentes, il est possible d'apercevoir un second arc-en-ciel dans le ciel, situé au-dessus de l'arc-en-ciel précédemment étudié. Il est même possible d'observer, dans de très rares occasions, un troisième arc-en-ciel qui s'ajoute aux deux précédents.
21. En considérant toujours des gouttelettes d'eau sphériques en suspension dans l'air, expliquer l'origine de ces différents arcs-en-ciel.

III. Fonctionnement d'un pluviomètre capacitif

La mesure des précipitations sur un territoire est importante pour prévoir l'évolution du débit de ses cours d'eau, et gérer de manière optimale les ressources en eau. Le volume de précipitations est généralement mesuré à l'aide d'un réseau de pluviomètres répartis sur le territoire, qui déterminent localement la hauteur d'eau tombée au sol par unité de surface pendant un intervalle de temps donné. Parmi les différents types de pluviomètre qui existent, nous allons étudier dans cette partie le fonctionnement d'un pluviomètre capacitif, qui est basé sur la mesure d'une capacité électrique.

III.1. Capacité du pluviomètre

Le pluviomètre capacitif est modélisé par un condensateur constitué de deux armatures cylindriques coaxiales d'axe et de hauteur , comme représenté sur la Figure 6 :
  • l'armature intérieure de rayon est portée au potentiel et possède une charge répartie sur sa surface ;
  • l'armature extérieure de rayon est portée au potentiel (avec ) et possède une charge répartie sur sa surface.
    On néglige les effets de bords dans cette étude, ce qui revient à considérer que la hauteur des armatures est infinie lors de la détermination du champ électrique. On considère le système de coordonnées cylindriques du repère ( ).
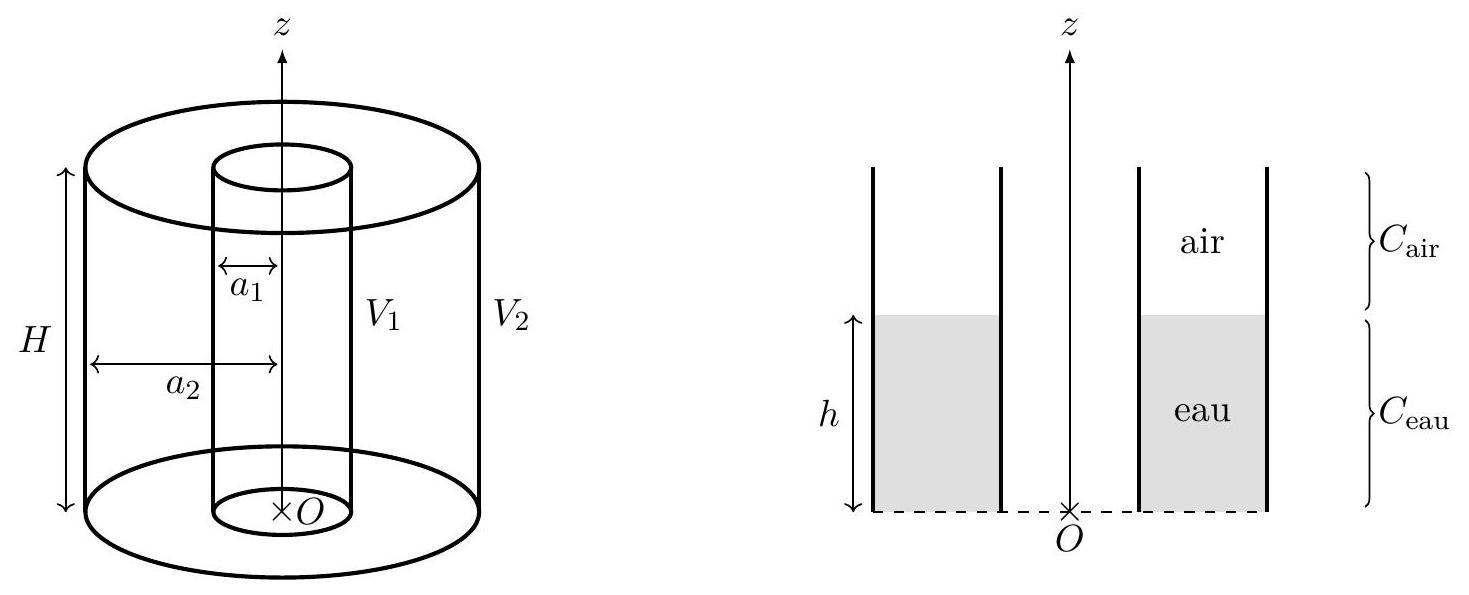
Figure 6 : Pluviomètre capacitif en l'absence d'eau (à gauche), et sa vue de coupe en présence d'eau (à droite).
Dans un premier temps, on étudie le pluviomètre en l'absence d'eau (Figure 6 à gauche). L'espace entre les deux armatures est alors rempli d'air, que l'on assimile au vide.
22. Justifier, de façon rigoureuse, que le champ électrique entre les deux armatures s'écrit sous la forme :
  1. À l'aide du théorème de Gauss, déterminer l'expression de entre les deux armatures en fonction des données de l'énoncé.
  2. Exprimer la capacité du condensateur en fonction de et .
  3. En déduire l'expression de en fonction de et de la permittivité diélectrique du vide .
On étudie maintenant le pluviomètre en présence d'eau (Figure 6 à droite). Celui-ci étant posé verticalement sur le sol, il s'est remplit progressivement d'eau lorsque de la pluie est tombée dans l'espace entre ses deux armatures cylindriques, et on note la hauteur d'eau qu'il contient à la fin d'une averse. L'eau étant un milieu diélectrique qui est caractérisé par sa permittivité diélectrique , et on peut montrer que le théorème de Gauss reste valable dans un tel milieu à condition de remplacer par .
26. Justifier que la capacité du condensateur en présence d'eau peut s'exprimer comme la somme :
avec la capacité de la partie du condensateur contenant de l'eau, et la capacité de la partie du condensateur contenant de l'air.
27. En déduire que la capacité du condensateur peut s'exprimer sous la forme :
avec et des constantes que l'on exprimera en fonction de et .

III.2. Conditionnement du pluviomètre

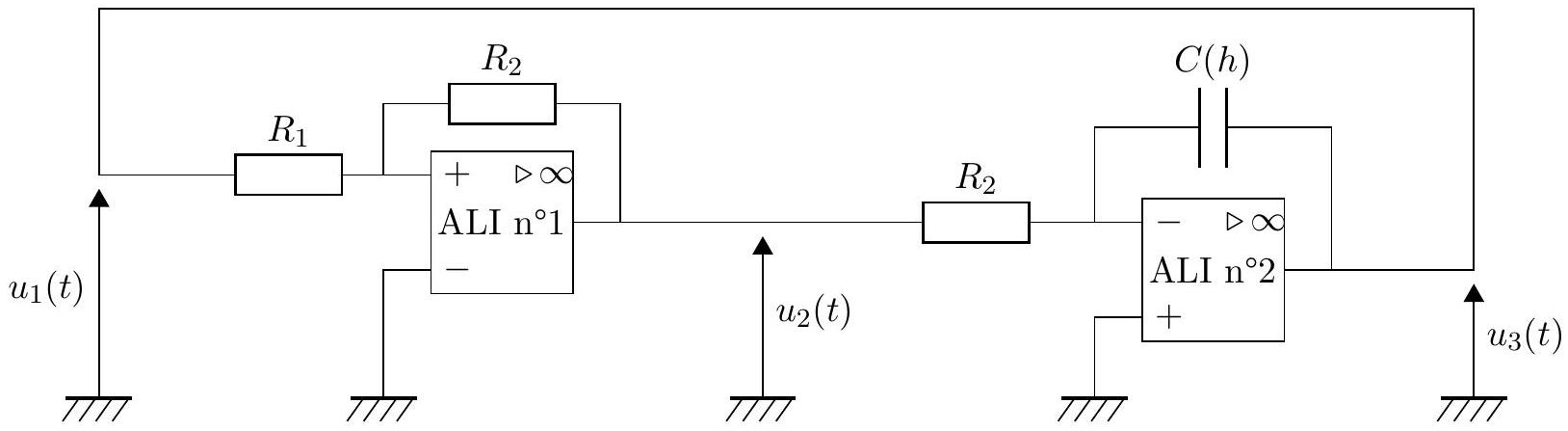
Pour mesurer la capacité électrique du pluviomètre, ce dernier est inséré dans le multivibrateur astable présenté en Figure 7, qui est constitué de deux amplificateurs linéaires intégrés (ALI). Nous allons montrer que la période des tensions électriques dans ce montage est proportionnelle à la capacité du pluviomètre.
Figure 7 : Multivibrateur astable réalisant le conditionnement du pluviomètre.
On suppose que les deux ALI de ce montage sont idéaux et alimentés par une tension continue. On note leur tension de saturation.
28. Rappeler les valeurs des courants de polarisation, de l'impédance d'entrée, de l'impédance de sortie, et du gain statique pour un ALI idéal.
On étudie tout d'abord la première partie du montage, comprise entre les tensions et sur la Figure 7.
29. Justifier que l'ALI fonctionne en régime saturé.
30. Exprimer le potentiel de l'entrée non-inverseuse de l'ALI en fonction de et .
31. En supposant que , déterminer la tension seuil correspondant au basculement de l'ALI .
32. En supposant que , déterminer la tension seuil correspondant au basculement de l'ALI .
On étudie maintenant la seconde partie du montage, comprise entre les tensions et sur la Figure 7.
33. Justifier que l'ALI fonctionne en régime linéaire.
34. Montrer que la tension peut s'exprimer sous la forme :
avec une constante positive que l'on exprimera en fonction des composants du montage.
On étudie enfin le montage dans son ensemble. On suppose que le potentiel en sortie de l'ALI bascule à à l'instant , les tensions vérifient donc : et .
35. Déterminer l'expression de la tension , tant que l'ALI n'a pas basculé, en fonction du temps , de la tension de saturation et des composants du montage.
36. Exprimer l'instant , où le potentiel en sortie de l'ALI bascule à , en fonction des composants du montage.
37. Déterminer l'expression de la tension , après le basculement de l'ALI , en fonction du temps , de la tension de saturation et des composants du montage.
38. Exprimer l'instant , où le potentiel en sortie de l'ALI bascule à nouveau à , en fonction des composants du montage.
39. Représenter graphiquement l'évolution des tensions et entre les instants et .
40. Exprimer la période des oscillations de ces tensions en fonction des composants du montage.

III.3. Mesure d'un volume de précipitations

Initialement vide, le pluviomètre s'est rempli d'une certaine hauteur d'eau après une averse où on suppose que la pluie est tombée verticalement. Le multivibrateur astable présente alors des tensions et de période .
41. Sachant que le pluviomètre ne contient que l'eau tombée dans l'espace entre ses deux armatures cylindriques, relier la hauteur d'eau tombée au sol par unité de surface à la hauteur d'eau dans le pluviomètre.
42. À l'aide des résultats précédents, déterminer l'expression de en fonction de , et .
On donne pour le pluviomètre : et .
43. Calculer la valeur de après cette averse à l'aide des données numériques.

IV. Remplissage d'une nappe phréatique

Une partie des eaux de pluie tombées au sol va s'infiltrer à travers les porosités des roches calcaires le constituant jusqu'à rejoindre des nappes phréatiques. Le renouvellement de l'eau présente dans ces nappes phréatiques est essentiel, car elles représentent aujourd'hui la principale source d'eau potable que nous consommons. À l'aide d'un modèle d'écoulement simple, nous allons estimer dans cette partie le temps mis par une gouttelette d'eau de pluie pour rejoindre une nappe phréatique située à un kilomètre de profondeur.
On modélise le sol poreux dans lequel s'écoule l'eau comme un ensemble de capillaires cylindriques verticaux de hauteur et de rayon . L'eau est assimilée à un fluide newtonien incompressible de viscosité dynamique et de masse volumique . L'étude des symétries et des invariances permet de supposer que la vitesse de l'eau dans un capillaire s'écrit en coordonnées cylindriques sous la forme :
avec l'axe vertical descendant, comme représenté sur la Figure 8.
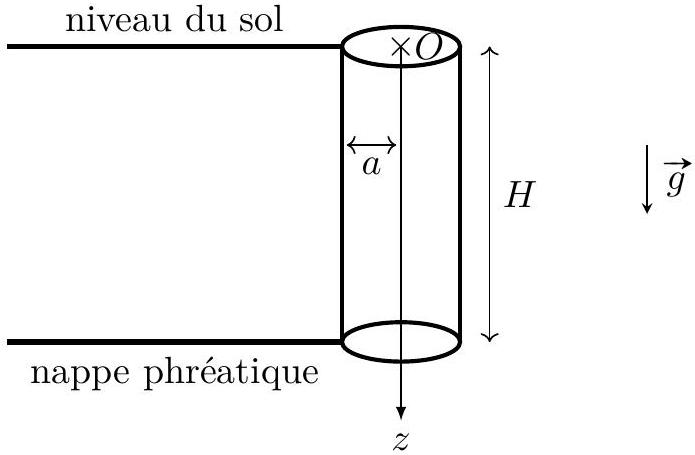
Figure 8 : Capillaire modélisant le sol poreux dans lequel s'écoule l'eau jusqu'à la nappe phréatique.
  1. Exprimer la condition aux limites imposée sur la vitesse de l'eau en l'assimilant à un fluide newtonien.
En supposant que la nappe phréatique communique avec l'atmosphère extérieure, sa pression s'égalise avec la pression atmosphérique, et on peut alors montrer que la vitesse de l'eau dans le capillaire vérifie l'équation :
où l'opérateur laplacien appliqué à la vitesse s'exprime sous la forme :
  1. Montrer que la vitesse de l'eau peut s'exprimer sous la forme :
avec une constante que l'on exprimera en fonction des données de l'énoncé.
46. Exprimer le temps minimal mis par une gouttelette d'eau pour rejoindre la nappe phréatique depuis le niveau du sol en fonction des données de l'énoncé, puis calculer sa valeur numérique.
47. Exprimer le débit volumique à travers une section du capillaire en fonction des données de l'énoncé.
48. En déduire l'expression de la vitesse moyenne à travers une section du capillaire.
49. Exprimer le temps moyen mis par une gouttelette d'eau pour rejoindre la nappe phréatique en fonction des données de l'énoncé, puis calculer sa valeur numérique.
En France, une << eau de source >> est une eau naturellement propre à la consommation humaine, qui est prélevée dans une nappe phréatique souterraine, puis mise en bouteille sans subir de traitement chimique. Tandis que l'eau de pluie est une eau très pure qui ne contient quasiment pas de minéraux, une eau de source présente une concentration en sels minéraux qui peut être assez importante.
50. À l'aide de la modélisation précédente, proposer une explication à cette différence de minéralisation entre l'eau de pluie et l'eau de source.

V. Production hydroélectrique d'un barrage

Une autre partie des eaux de pluie tombées au sol va ruisseler jusqu'à atteindre différents cours d'eau (ruisseau, rivière, fleuve...). Pour récupérer l'énergie renouvelable de ces eaux qui regagnent les mers et les océans, des barrages hydroélectriques ont été édifiées sur de nombreux cours d'eau dans le monde. Ces centrales hydroélectriques fournissent actuellement de la production mondiale d'électricité, ce qui correspond à une puissance d'environ . Le barrage le plus haut du monde est le barrage de Jinping I, qui est construit sur la rivière Yalong dans la province du Sichuan en Chine. Il s'agit d'un barrage-voute en béton de 305 m de haut constitué d'un arc-de-cercle de 568 m de long. Au niveau du
barrage, le débit volumique de la rivière Yalong est en moyenne de . Dans cette partie, nous allons estimer la résultante des forces de pression qui s'exercent sur un tel ouvrage lorsque son réservoir d'eau est rempli, et la puissance hydroélectrique qu'il est capable de récupérer.
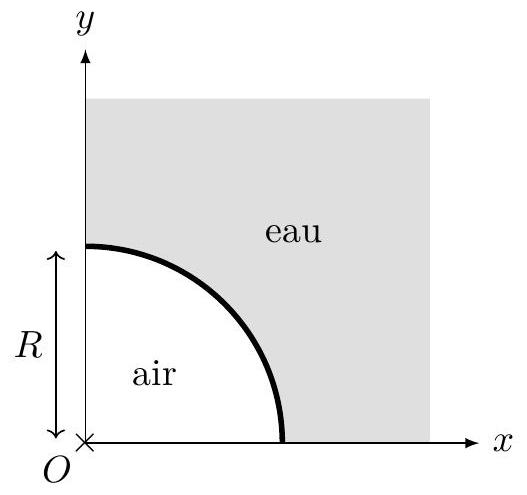
On modélise le barrage-voute par un quart de cylindre d'axe ( ) vertical ascendant, de rayon et de hauteur , comme représenté sur la Figure 9. On suppose que son réservoir rempli d'eau peut se vider dans un cours d'eau situé en contrebas à l'altitude . La pression de l'air est supposée uniforme dans tout l'espace et égale à la pression atmosphérique bar.
Figure 9 : Barrage-voute en vue de dessus (à gauche), et en vue de coupe (à droite).
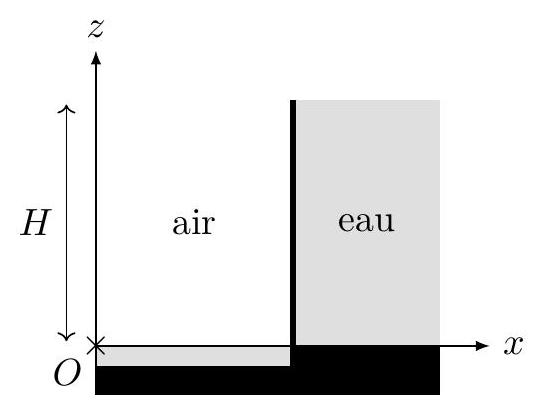
Figure 9 : Barrage-voute en vue de dessus (à gauche), et en vue de coupe (à droite).
  1. À l'aide d'arguments de symétrie, déterminer la direction de la résultante des forces de pression qui s'exercent sur le barrage, puis représenter le sens de cette résultante sur un schéma en vue de dessus.
  2. Exprimer la résultante des forces de pression exercées par l'air sur le barrage en fonction de et .
  3. En supposant que l'eau est un fluide incompressible, établir l'expression du champ de pression dans l'eau.
  4. Exprimer la résultante des forces de pression exercées par l'eau sur le barrage en fonction de et .
  5. En déduire que la norme de la résultante des forces de pression qui s'exercent sur le barrage s'exprime :
  1. Calculer numériquement la norme de cette résultante pour le barrage de Jinping I.
En pratique, le maintien de la structure en béton d'un barrage-voute est assuré par un report des forces de pression vers ses appuis latéraux.
57. À partir des données de l'énoncé, estimer numériquement la puissance hydroélectrique moyenne que peut récupérer le barrage de Jinping I.
58. Comparer l'ordre de grandeur de cette puissance à celle générée par une centrale nucléaire.
Fin de l'épreuve
Banque PT Physique A PT 2024 - Version Web LaTeX | WikiPrépa | WikiPrépa